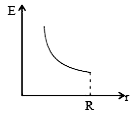
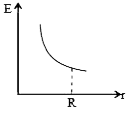
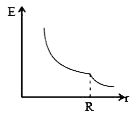
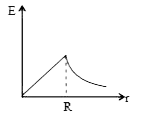
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A conducting shell of radius R carries charge–Q. A point charge +Q is ...
Text Solution
|
- A thin spherical conducting shell of radius R has a charge q. Another ...
Text Solution
|
- A conducting shell of radius R carries charge -Q. A point charge +Q is...
Text Solution
|
- A charge q is placed at a distance of 2R from the centre of a spherica...
Text Solution
|
- A point charge Q is placed inside a conducting spherical shell of inne...
Text Solution
|
- A point charge Q is placed inside a conducting spherical shell of inne...
Text Solution
|
- A thin spherical conducting shell of radius R has a charge q. Another ...
Text Solution
|
- A point charge Q is placed inside a conducting spherical shell of inne...
Text Solution
|
- A point charge q is placed inside a conducting spherical shell of inne...
Text Solution
|