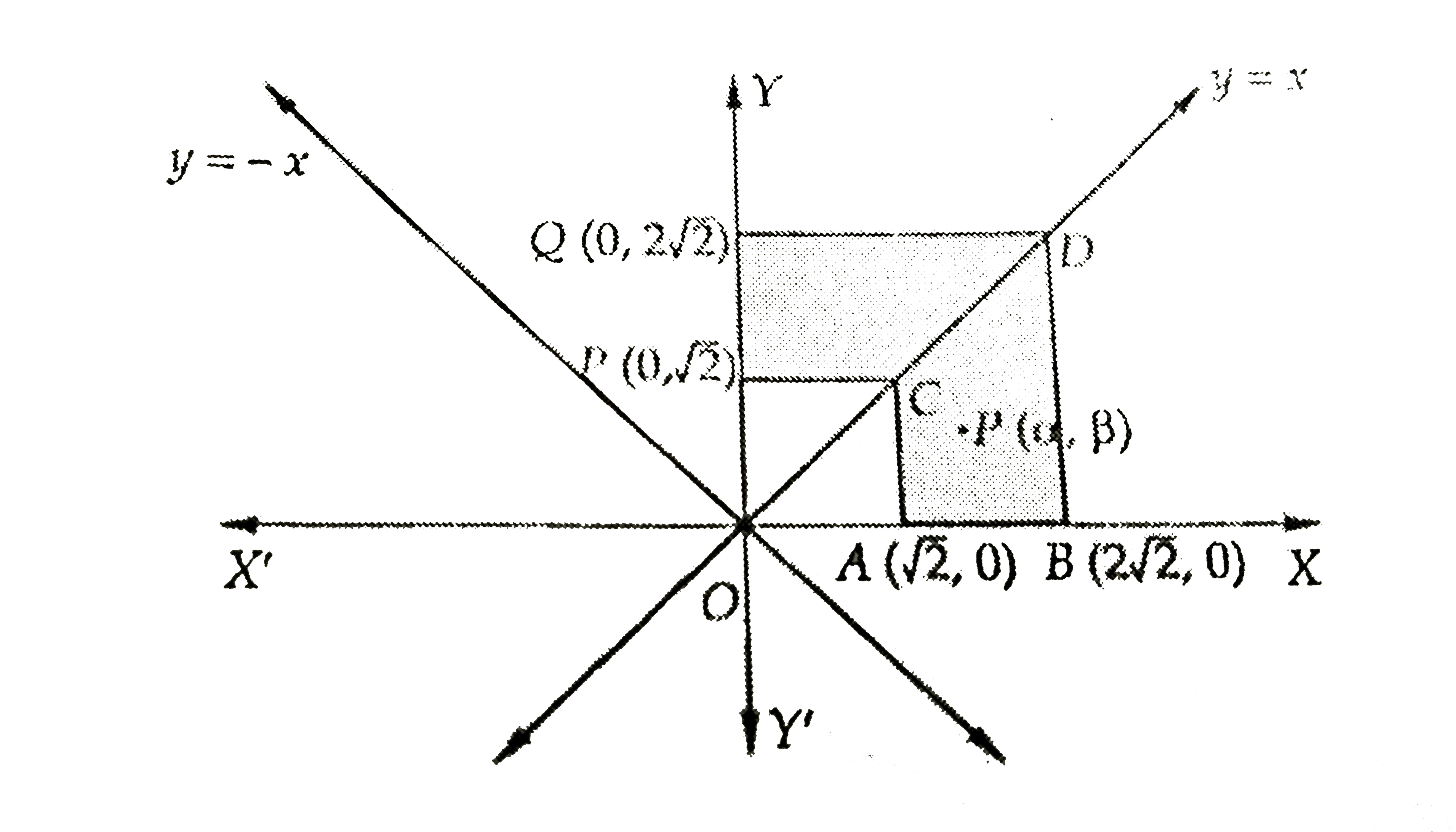
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
STRAIGHT LINES
OBJECTIVE RD SHARMA ENGLISH|Exercise Section-1 Solved MCQs (Example)|1 VideosSTRAIGHT LINES
OBJECTIVE RD SHARMA ENGLISH|Exercise SECTION - II (ASSERTION - REASON TYPE MCQs)|14 VideosSTRAIGHT LINES
OBJECTIVE RD SHARMA ENGLISH|Exercise ILLUSTRATION 18|1 VideosSETS
OBJECTIVE RD SHARMA ENGLISH|Exercise Chapter Test|30 Videos
Similar Questions
Explore conceptually related problems
OBJECTIVE RD SHARMA ENGLISH-STRAIGHT LINES-Section I - Solved Mcqs
- Prove that the locus of the centroid of the triangle whose vertices ar...
Text Solution
|
- The locus of a point which moves such that difference of its distance ...
Text Solution
|
- If the sum of the distances of a point from two perpendicular lines in...
Text Solution
|
- distance of the lines 2x-3y-4=0 from the point (1, 1) measured paralel...
Text Solution
|
- ABC is an isosceles triangle. If the coordinates of the base are B(1,3...
Text Solution
|
- The co-ordinate axes are rotated about the origin O in the counter-clo...
Text Solution
|
- If the equation of the locus of a point equidistant from the points (a...
Text Solution
|
- Let A(2,-3) and B(-2,1) be the vertices of Delta A B Cdot If the ...
Text Solution
|
- Find the equation of the straight line passing through the point (4,3)...
Text Solution
|
- about to only mathematics
Text Solution
|
- A straight line L through the point (3,-2) is inclined at an angle 60^...
Text Solution
|
- IfA(2,-3) and B(-2, 1) are two vertices of a triangle and third vertex...
Text Solution
|
- A ray of light along x+sqrt(3) y = sqrt(3) gets reflected upon reachin...
Text Solution
|
- Let P S be the median of the triangle with vertices P(2,2),Q(6,-1)a...
Text Solution
|
- For a point P in the plane, let d1(P)a n dd2(P) be the distances of th...
Text Solution
|
- The area of region bounded by the lines y=x,y=0 and x=sin^-1(a^4+1)+co...
Text Solution
|
- A ray of light is incident along a line which meets another line, 7x-...
Text Solution
|
- Two sides of a rhombus are along the lines x-y+1=0 and 7x-y-5=0. If it...
Text Solution
|
- In a triangle ABC , right angled at the vertex A , if the position vec...
Text Solution
|
- If a variable line drawn through the intersection of the line x/3+y/4=...
Text Solution
|