Similar Questions
Explore conceptually related problems
Recommended Questions
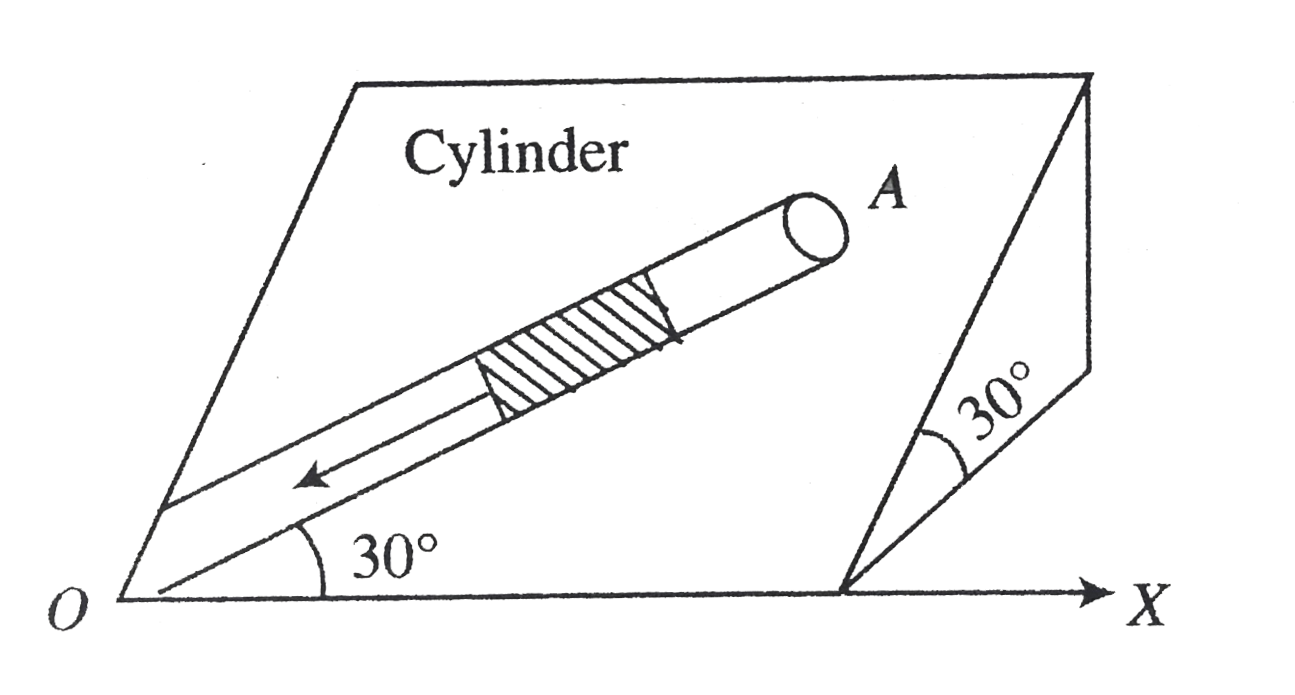
- An inclined plane makes an angle 30^(@) with the horizontal. A groove ...
Text Solution
|
- An inclined plane makes an angle 30^(@) with the horizontal. A groove ...
Text Solution
|
- A body is allowed to slide from the top along a smooth inclined plane ...
Text Solution
|
- A smooth inclined plane is inclined at an angle theta with the horizon...
Text Solution
|
- A body of mass 10kg is placed on a smooth inclined plane making an ang...
Text Solution
|
- A block slides down a frictionless, inclined plane that makes a 30^(@)...
Text Solution
|
- A solid cylinder rolls up an inclined plane of angle of inclination 30...
Text Solution
|
- A cylinder of mass m is kept on an inclined plane haivng an angle of i...
Text Solution
|
- A cylinder rolls down an inclined plane of inclination 30^@, the accel...
Text Solution
|