A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Recommended Questions
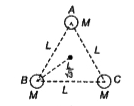
- Three identical bodies of mass M are located at the vertices of an eq...
Text Solution
|
- Three identical particles each of mass "m" are arranged at the corners...
Text Solution
|
- Three particles each of mass m are kept at vertices of an equilateral ...
Text Solution
|
- Three particle each of mass m, are located at the vertices of an equil...
Text Solution
|
- Three indentical bodes of mass M are locatd at the verticles of a...
Text Solution
|
- Three particles each of mass m are kept at the vertices of an euilater...
Text Solution
|
- Three mass ‘m’ each are kept at corner of a equilateral triangle and a...
Text Solution
|
- a भुजा वाले एक समबाहु त्रिभु के प्रत्येक कोने पर द्रव्यमान का एक कण...
Text Solution
|
- L भुजा के समबाहु त्रिभुज के शीर्षो पर प्रत्येक M द्रव्यमान के तीन समान...
Text Solution
|