Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-INTRODUCTION TO MATHEMATICAL MODELLING-EXAMPLE
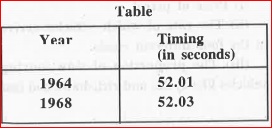
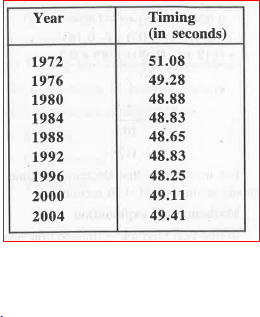
- We have given the timings of the gold medalists in the 400-metre race ...
Text Solution
|
- I travelled 432 kilometres on 48 litres of petrol in my car. I have to...
Text Solution
|
- Let Sudhir invested Rs. 15000 at 8% simple interest. He wants to buy w...
Text Solution
|
- A boat can go 20 km upstream and 30 km downstream in 3 hours. It can g...
Text Solution
|
- Suppose you have a room of length 6 m and breadth 5 m. You want to cov...
Text Solution
|