Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-LINES AND ANGLES-EXAMPLE
- In Fig. 6.9, lines PQ and RS intersect each other at point O. If angle...
Text Solution
|
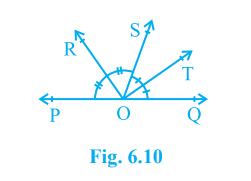
- In Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle...
Text Solution
|
- In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that angle POQ + ...
Text Solution
|
- In Fig. 6.24, if PQ || RS, angle MXQ = 135^@ and angle MYR = 40^@, fin...
Text Solution
|
- If a transversal intersects two lines such that the bisectors of a pai...
Text Solution
|
- In Fig. 6.27, AB || CD and CD || EF. Also EA bot AB. If angle BEF = 5...
Text Solution
|
- In Fig. 6.37, if QT bot PR, angle TQR = 40^@ and angle SPR = 30^@, fin...
Text Solution
|
- In Fig. 6.38, the sides AB and AC of Delta ABC are produced to points ...
Text Solution
|