Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-TRIANGLES-EXAMPLE
- if a line intersects sides AB and AC of a DeltaABC at D and E respecti...
Text Solution
|
- ABCD is a trapezium with AB II DC, E and F are paints on non-parallel ...
Text Solution
|
- In (PS)/(SQ)=(PT)/(TR) and angle PST= angle PRQ. Prove that PQR is an ...
Text Solution
|
- Observe Fig. 6.30 and then find angle P.
Text Solution
|
- In Fig, OA . OB = OC . OD. Show that angle A=angle C and anlge B=angle...
Text Solution
|
- A girl of height 90cm cm is walking away from the base of a lamp-post...
Text Solution
|
- In Fig, the line segment XY is parallel to side AC of Delta ABC and it...
Text Solution
|
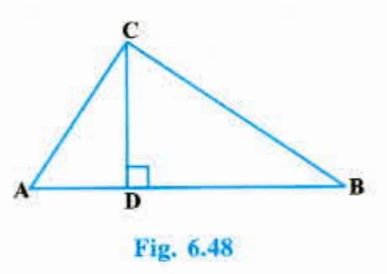
- In Fig. 6.48, angle ACB = 90^@ and CD bot AB. Prove that (BC^2)/(AC^2)...
Text Solution
|
- A ladder is placed against a wall such that its foot is at a distance ...
Text Solution
|
- In Fig if AD bot BC, prove that AB^2 + CD^2 = BD^2 + AC^2.
Text Solution
|
- BL and CM are medians of a triangle ABC right angled at A. Prove that ...
Text Solution
|
- O is any point inside a rectangle ABCD (see Fig. 6.52). Prove that OB^...
Text Solution
|