Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
PSEB-CIRCLES-EXAMPLE
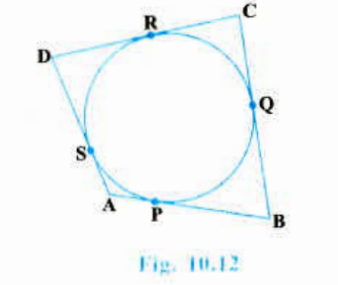
- A quadrilateral ABCD is drawn to circumscribe a circle(seeFig).Prove t...
Text Solution
|
- Prove that in two concentric circles, the chord of the larger circle, ...
Text Solution
|
- Two tangents TP and TQ are drawn to a circle with centre O from an ext...
Text Solution
|
- PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents ...
Text Solution
|