Text Solution
Verified by Experts
Topper's Solved these Questions
QUADRILATERALS
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8a|29 VideosQUADRILATERALS
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 8b|15 VideosQUADRILATERALS
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Questions)|5 VideosPROBABILITY
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (very Short Answer /short Answer Questions)|10 VideosSTATISTICS
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise|12 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-QUADRILATERALS-Problems From NCERT/exemplar
- Show that if the diagonals of a quadrilateral bisect each other at ...
Text Solution
|
- Diagonal AC of a paraleligram ABCD bisects angleA (sec figure). Show t...
Text Solution
|
- ABCD is a rectangle in which diagonal AC bisects angleA as well as ang...
Text Solution
|
- In parallelogram ABCD two points P and Q are taken on diagonal BD such...
Text Solution
|
- P, Q, R and S are respectively the mid-points of the sides AB, BC, CD ...
Text Solution
|
- Show that the line segments joining the mid-points of the opposite s...
Text Solution
|
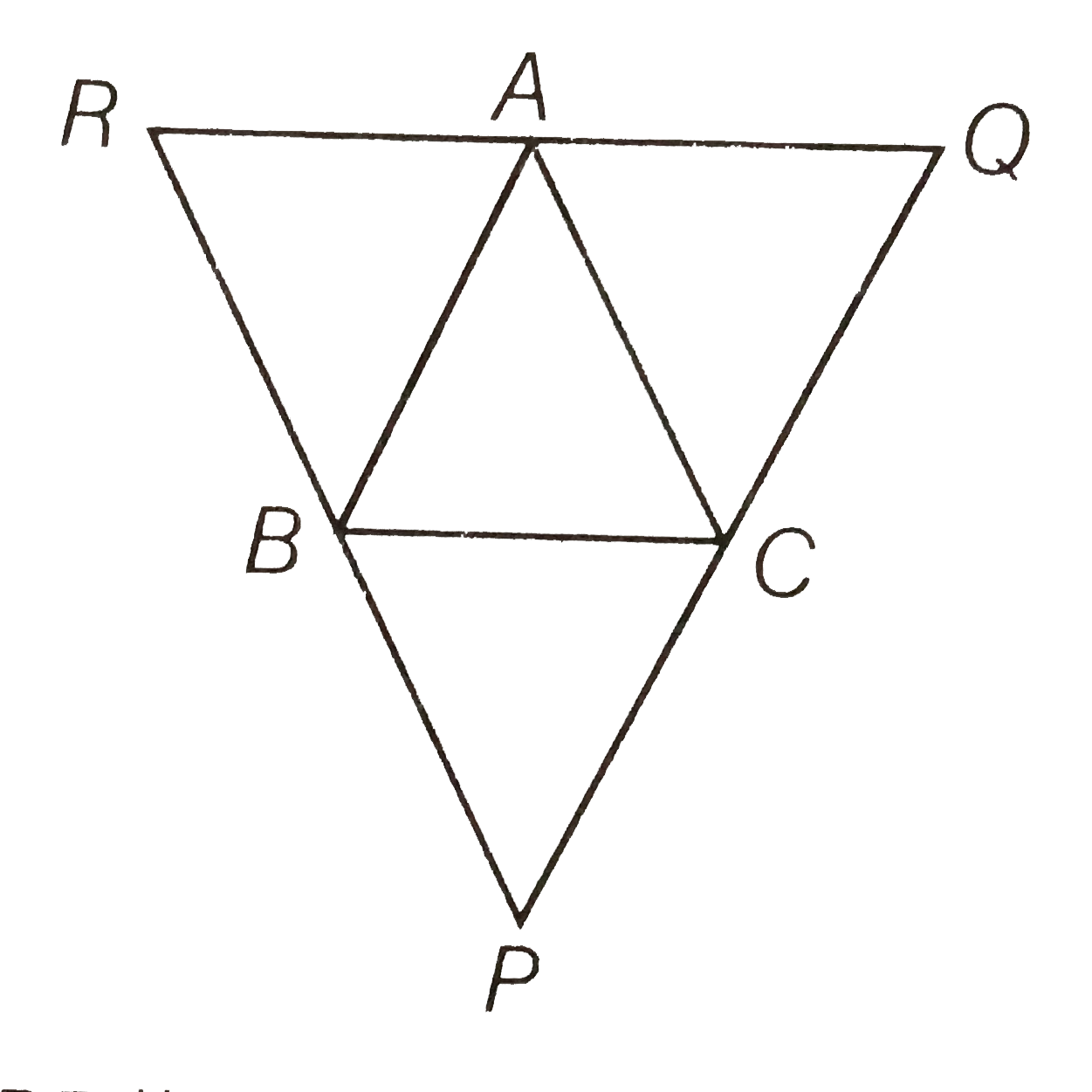
- Through A, B and C lines RQ, PR and QP have been drawn, respectively p...
Text Solution
|
- In figure, P is the mid-point of side BC of a parallelogram ABCD such ...
Text Solution
|
- P and Q are the mid-point of the opposite sides AB and CD of a paralle...
Text Solution
|
- In figure, AB||DE, AB=DE, AC||DF and AC=DF. Prove that BC||EF and BC=E...
Text Solution
|
- Prove that the quadrilateral formed by the bisectors of the angles of ...
Text Solution
|