Text Solution
Verified by Experts
Topper's Solved these Questions
AREA OF PARALLELOGRAMS AND TRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise|34 VideosAREA OF PARALLELOGRAMS AND TRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (very Short Answer Questions)|10 VideosAREA OF PARALLELOGRAMS AND TRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Question)|5 VideosCIRCLE
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Questions )|5 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-AREA OF PARALLELOGRAMS AND TRIANGLES-Problems From NCERT/exemplar
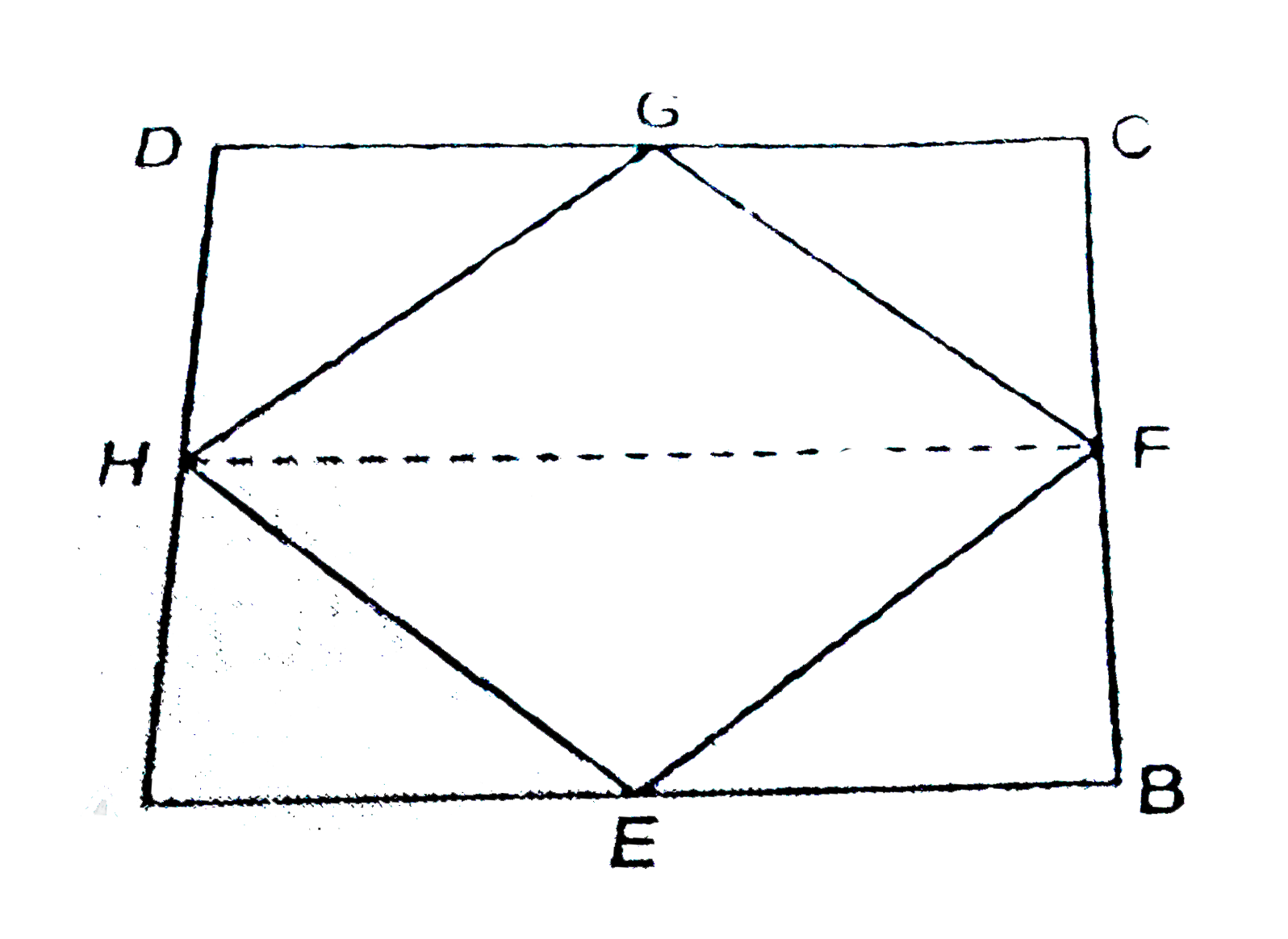
- If E ,\ F ,\ G\ a n d\ H are respectively the mid-points of the side...
Text Solution
|
- In Figure, P is a point in the interior of a parallelogram A B C Dd...
Text Solution
|
- In Fig. 9.24, ABC and ABD are two triangles on the same base AB. If l...
Text Solution
|
- P and Q are any two points lying on the sides DC and AD respectively ...
Text Solution
|
- A villager Itwari has a plot of land of the shape of a quadrilatera...
Text Solution
|
- Diagonals AC and BD of a quadrilateral ABCD intersect at O in such ...
Text Solution
|
- In the figure, PSDA is a parallelogram. Points Q and R are taken on PS...
Text Solution
|
- X and Y are points on the side LN of the triangle LMN such that LX = X...
Text Solution
|
- ABCD is a square. E and F are respectively the mid-points of BC and CD...
Text Solution
|
- If the mid-points of the sides of a quadrilateral are joined in order,...
Text Solution
|
- In figure, CD || AE and CY || BA. Prove that ar (DeltaCBX) = ar (Delta...
Text Solution
|
- In figure, ABCD and AEFD are two parallelograms. Prove that ar (DeltaP...
Text Solution
|