Home
Class 9
MATHS
In the given figure, PQRS is a parallelo...

In the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of `(||gm XQRY) : " area "(Delta QSR)`

Text Solution

Verified by Experts

The correct Answer is:
`1 : 1`
Promotional Banner

Topper's Solved these Questions

  • AREA OF PARALLELOGRAMS AND TRIANGLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Question)|5 Videos

  • AREA OF PARALLELOGRAMS AND TRIANGLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (very Short Answer Questions)|10 Videos

  • CIRCLE

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Questions )|5 Videos

Similar Questions

Explore conceptually related problems

In the given figure, ABCD is a parallelogram. Find the area of DeltaAED

PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR. Show that LM and QS bisect each other.

In the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.

In Figure, A B C D is a parallelogram and X ,Y are the mid-points of sides A B and D C respectively. Show that A X C Y is a parallelogram.

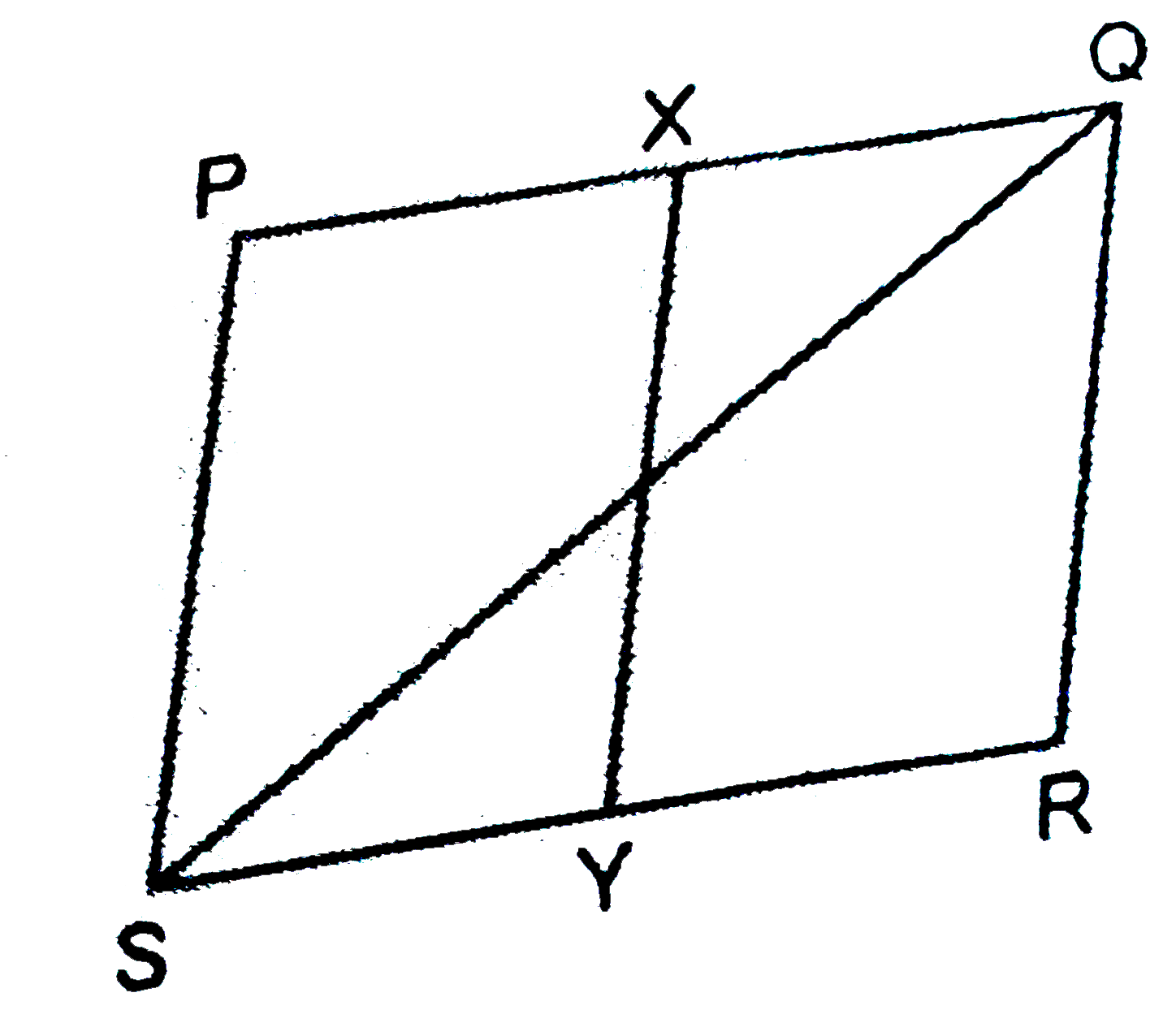
In the given figure, D is the mid-point of BC, E is the mid-point of BD and O is the mid-point of AE. Find the ratio of area of Delta BOE and DeltaABC

In A B C ,\ D and E are the mid-points of A B and A C respectively. Find the ratio of the areas of A D E and A B C .

In the given figure, ABCD is a parallelogram whose area is 60 cm^(2) . Find the area of DeltaACB

ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively. Prove that area of triangle APQ= (1)/(8) of the area of parallelogram ABCD.

ABCD is a parallelogram. P and Q are the mid-points of sides AB and AD reapectively. Prove that area of triangle APQ= (1)/(8) of the area of parallelogram ABCD.

In Figure, A B C D is a parallelogram and X ,Y are the mid=points of sides A B and D C respectively. Show that A X C Y is a parallelogram. Figure