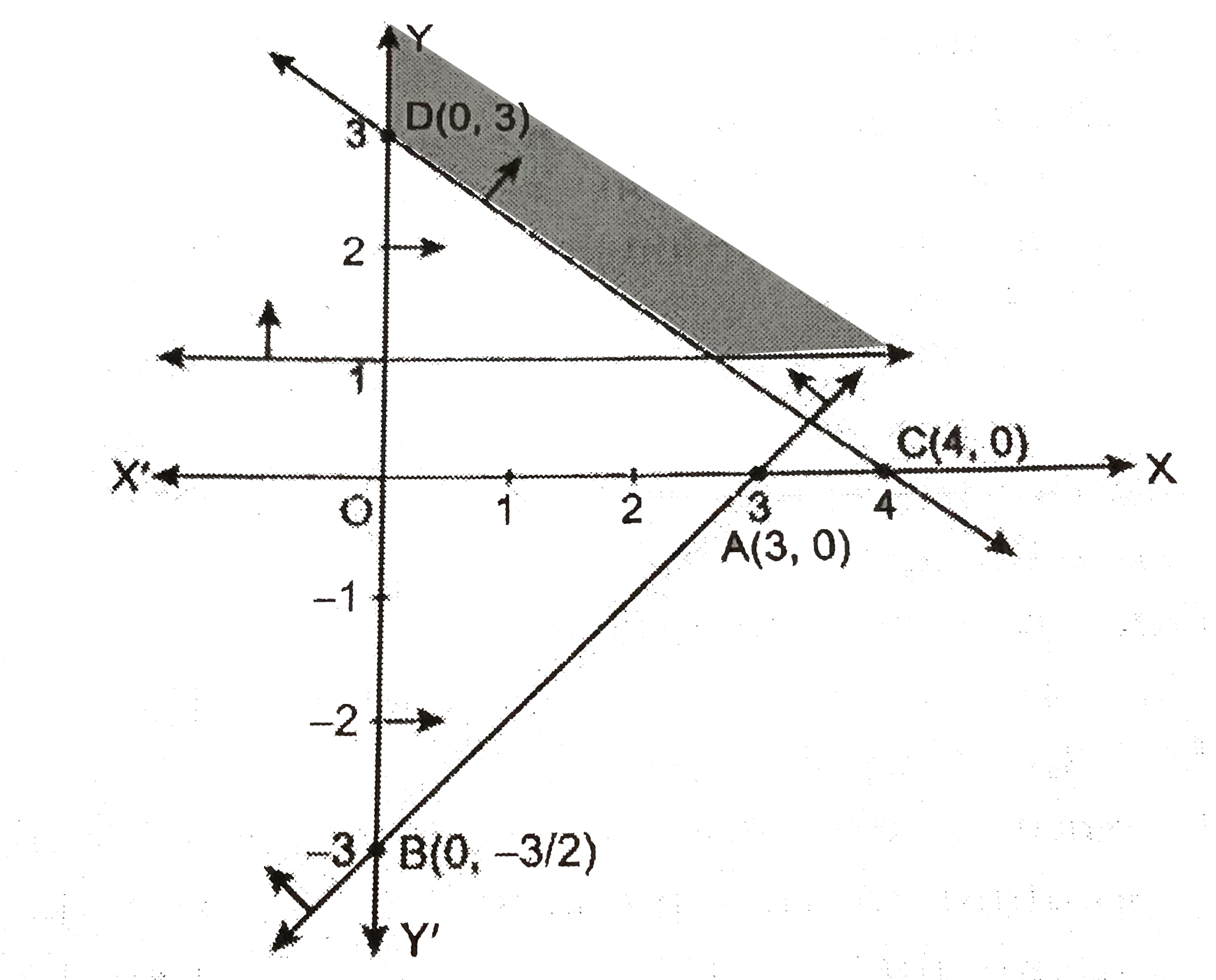Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
LINEAR INEQUALITIES
NAGEEN PRAKASHAN ENGLISH|Exercise MISCELLANEOUS EXERCISE|14 VideosLINEAR INEQUALITIES
NAGEEN PRAKASHAN ENGLISH|Exercise EXERCISE|76 VideosLIMITS AND DERIVATIVES
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|30 VideosMATHEMATICAL REASONING
NAGEEN PRAKASHAN ENGLISH|Exercise Misellaneous exercise|7 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-LINEAR INEQUALITIES-NCERT QUESTION
- 2x - 3y gt 6
Text Solution
|
- -3x + 2y ge - 6
Text Solution
|
- 3y -5x lt 30
Text Solution
|
- y lt - 2
Text Solution
|
- x gt -3
Text Solution
|
- plot x ge 3, y ge 2
Text Solution
|
- 3x + 2y le 12, x ge 1, y ge 2
Text Solution
|
- 2x + y ge 6, 3x + 4y le 12
Text Solution
|
- x + y ge 4, 2x - y lt 0
Text Solution
|
- Solve the linear inequalities 2x - y gt 1 , x - 2y lt 1
Text Solution
|
- x + y le 6, x + y ge 4
Text Solution
|
- 2x + y ge 8, x + 2y ge 10
Text Solution
|
- Find common region of given inequation x + y le 9, x gt y, xge 0
Text Solution
|
- Solve the system of inequalities graphically :5x+4ylt=20 ,xgeq1,ygeq2
Text Solution
|
- Find the common region of given inequation 3x + 4y le 60, x + 3y le 30...
Text Solution
|
- Solve the linear inequalities. 2x + y ge 4, x + y le 3, 2x - 3y le 6
Text Solution
|
- Show that the following system of linear inequalities has no solutin ...
Text Solution
|
- 4x + 3y le 60, y ge 2x, x ge 3, x, y ge 0
Text Solution
|
- Show the common solution of given inequalities and shade the region bo...
Text Solution
|
- x + 2y le 10, x + y ge 1, x-y le 0, x ge 0, yge 0
Text Solution
|