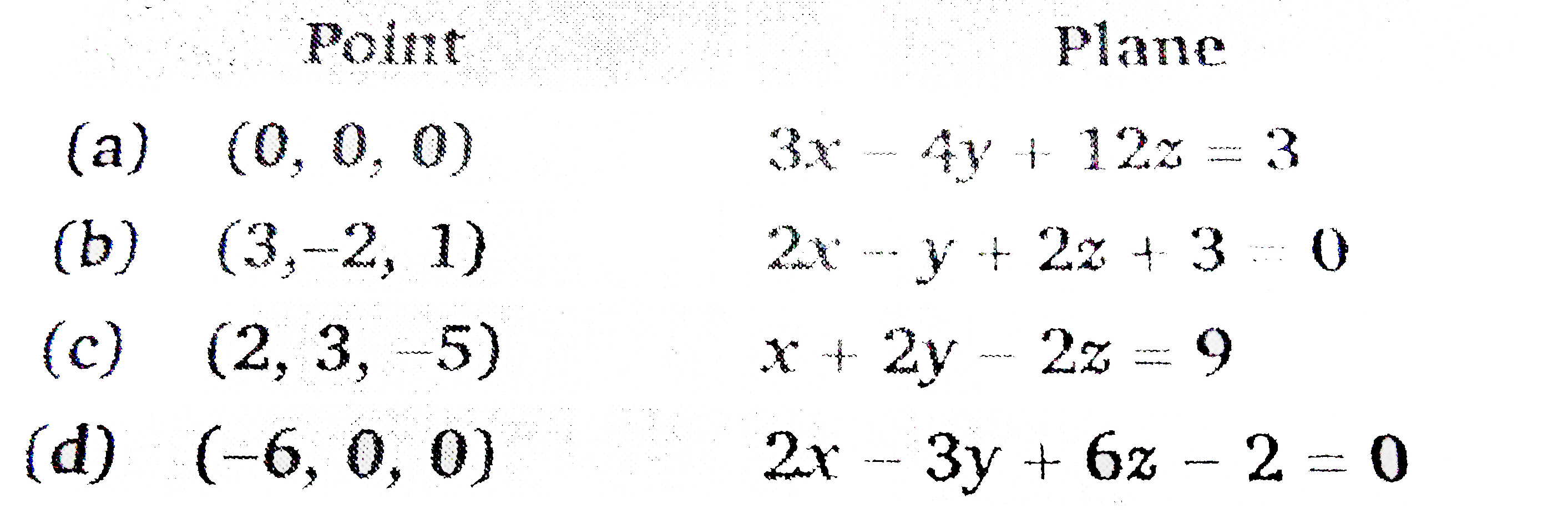Text Solution
Verified by Experts
Topper's Solved these Questions
THREE-DIMENSIONAL GEOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|23 VideosTHREE-DIMENSIONAL GEOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 11.2|17 VideosRELATIONS AND FUNCTIONS
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|19 VideosVECTORS
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|19 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-THREE-DIMENSIONAL GEOMETRY -Exercise 11.3
- In each of the following cases, determine the direction cosines of th...
Text Solution
|
- Find the vector equation of a plane which is at a distance of 7 units...
Text Solution
|
- Find the Cartesian equations of the following planes whose vector equa...
Text Solution
|
- In the following cases, find the coordinates of the foot of the perpe...
Text Solution
|
- Find the vector and Cartesian equation of the plane that passes throug...
Text Solution
|
- Find the equations of the planes that passes through three points. ...
Text Solution
|
- Find the intercepts cut off by the plane 2x + y- z = 5.
Text Solution
|
- Find the equation of the plane with intercept 3 on the y-axils and ...
Text Solution
|
- Find the equation of the plane through the intersection of the plan...
Text Solution
|
- Find the equation of the plane passing through the intersection of the...
Text Solution
|
- Find the vector equation of the plane through the line of intersection...
Text Solution
|
- Find the direction cosines of the unit vector perpendcular to the plan...
Text Solution
|
- In the following cases, determine whether the given planes are para...
Text Solution
|
- In the following cases, find the distance of each of the given points...
Text Solution
|