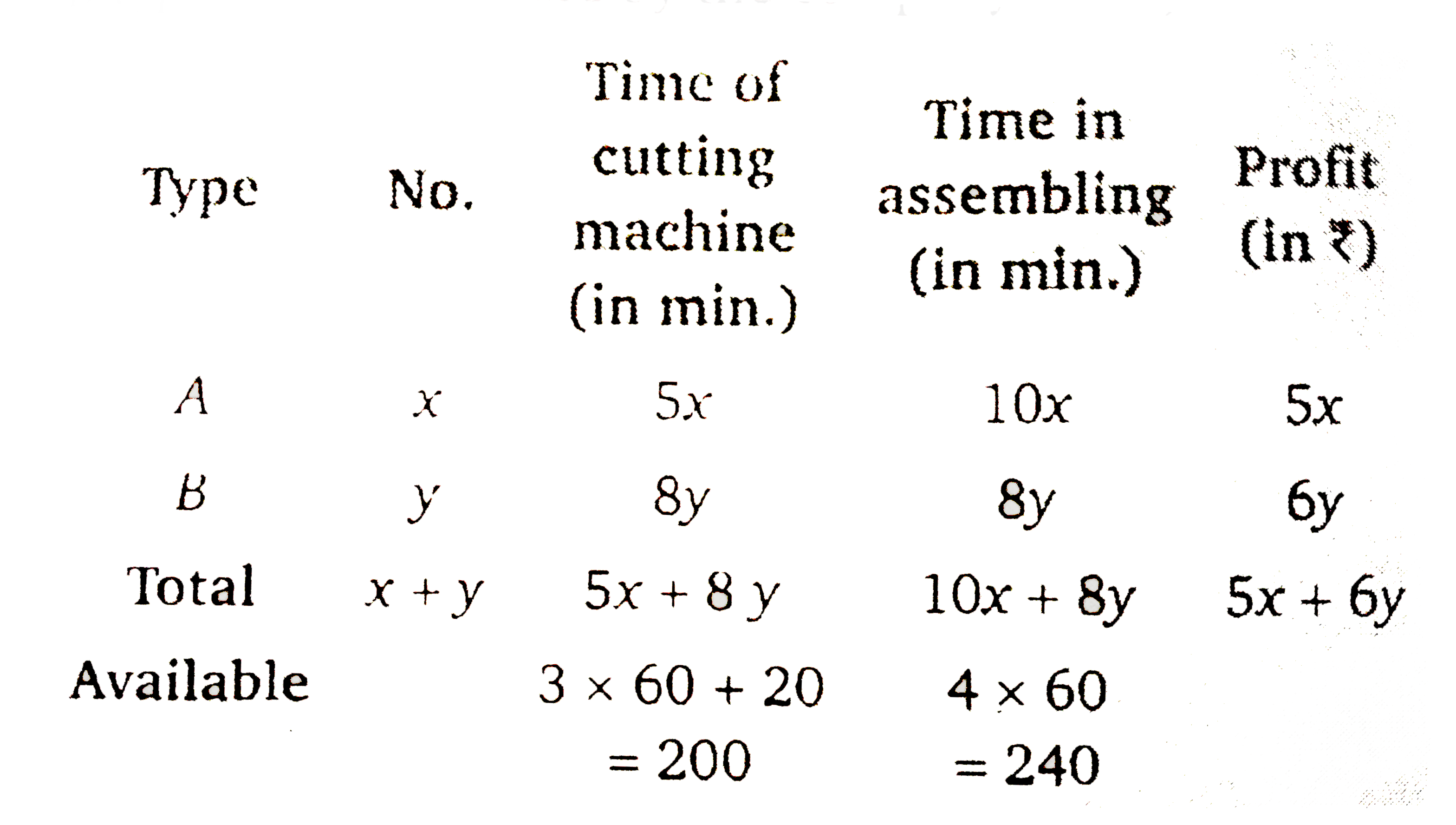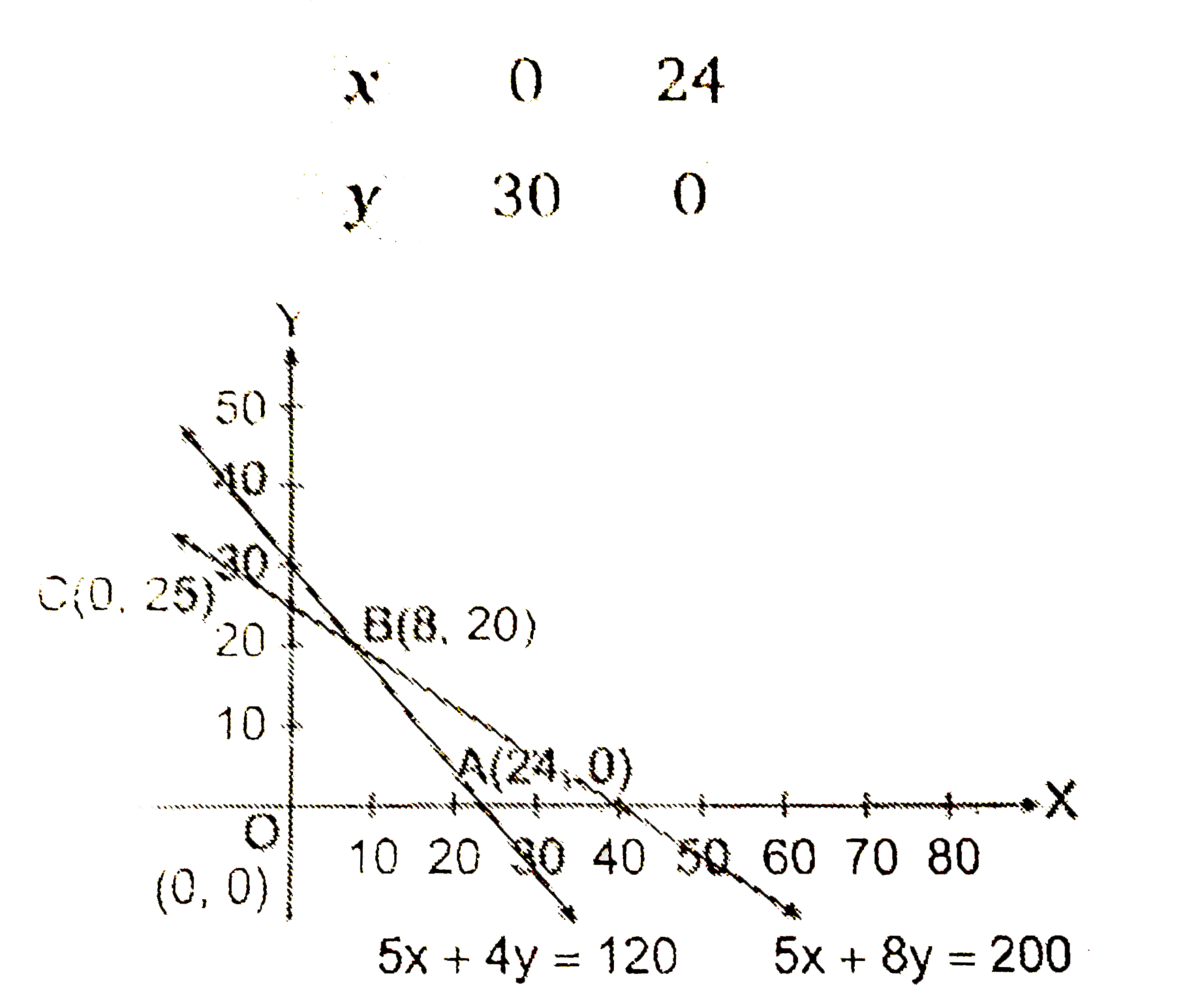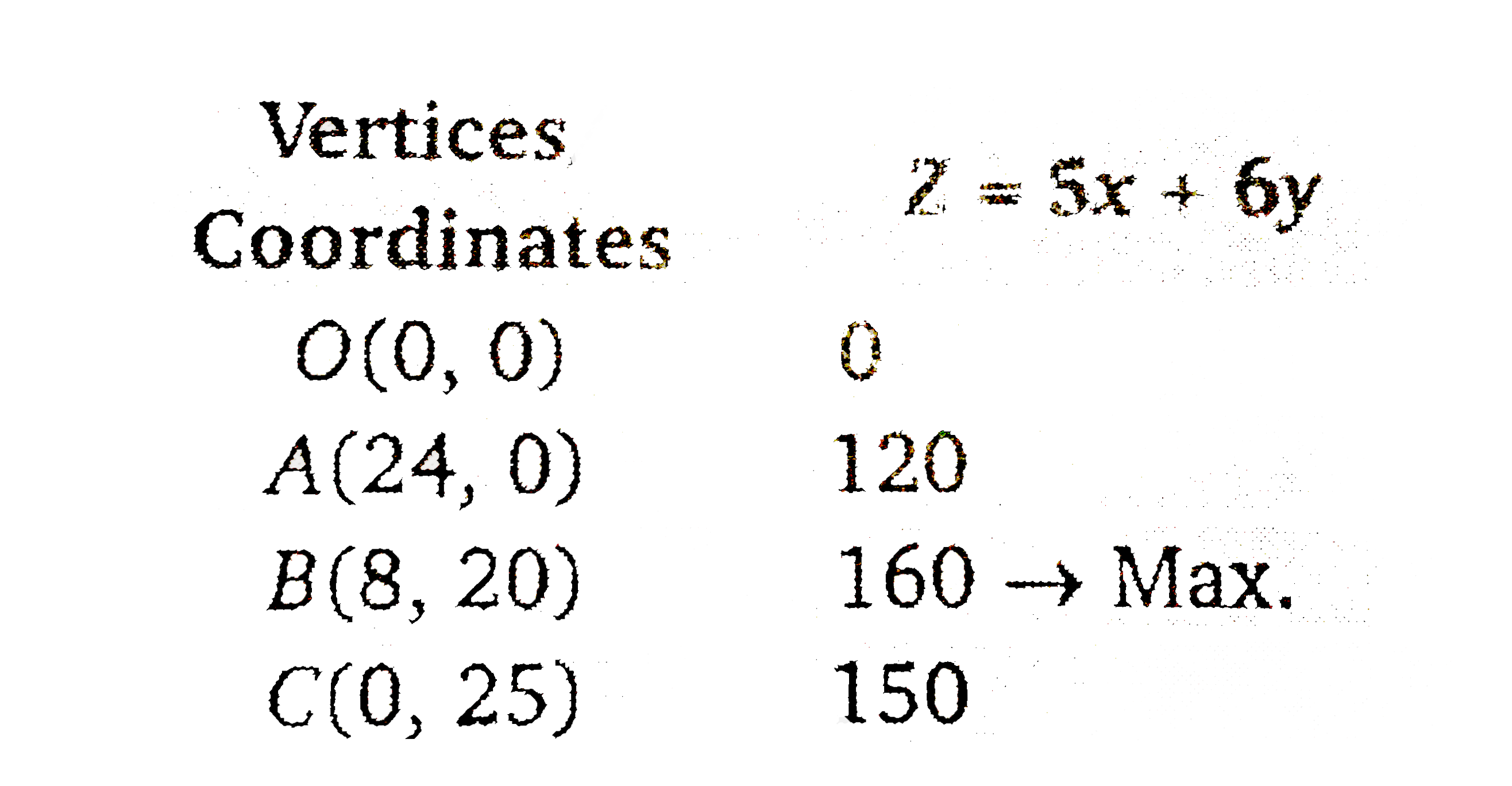Text Solution
Verified by Experts
Topper's Solved these Questions
LINEAR PROGRAMMING
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise|9 VideosLINEAR PROGRAMMING
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 12.1|10 VideosINVERES TRIGONOMETRIC FUNCTIONS
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exercise (prove That )|9 VideosMATRICES
NAGEEN PRAKASHAN ENGLISH|Exercise Miscellaneous Exerice|15 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-LINEAR PROGRAMMING-Exercise 12.2
- Reshma wishes to mix two types of food P and Q in such a way that t...
Text Solution
|
- One kind of cake requires 200 g of flour and 25 g of fat, and anoth...
Text Solution
|
- A factory makes tennis rackets and cricket bats. A tennis racket ta...
Text Solution
|
- A manufacturer produces nuts and bolts. It takes 1 hour of work on m...
Text Solution
|
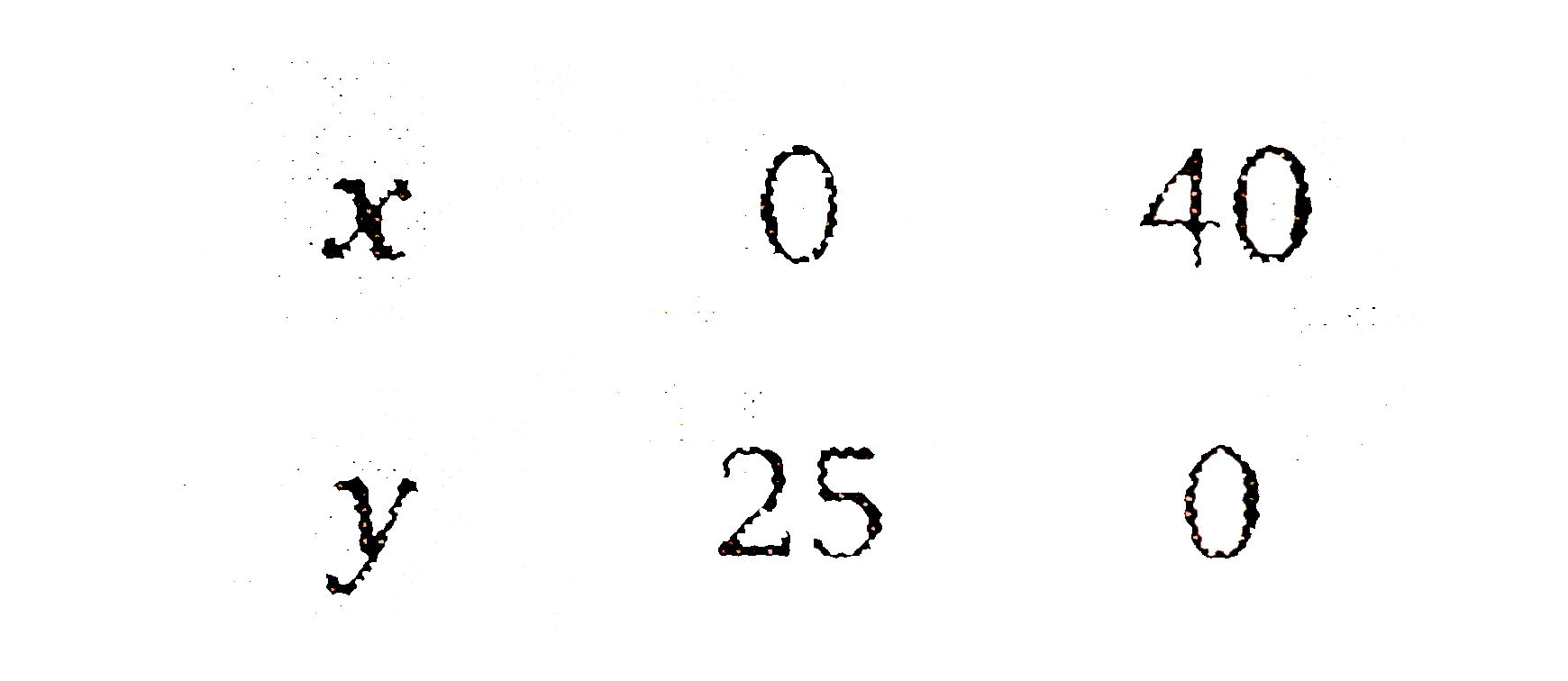
- A factory manufactures two types of screws, A and B. Each type of s...
Text Solution
|
- A cottage industry manufactures pedestal lamps and wooden shades, e...
Text Solution
|
- A company manufactures two types of novelty souvenirs made of plywo...
Text Solution
|
- A merchant plans to sell two types of personal computers - a deskto...
Text Solution
|
- A diet is to contain at leat 80 units of vitamin A and 100 units of mi...
Text Solution
|
- There are two types of fertilizers F(1) and F(2).F(1) consists of 10% ...
Text Solution
|
- The corner points of the feasible region determined by the following ...
Text Solution
|