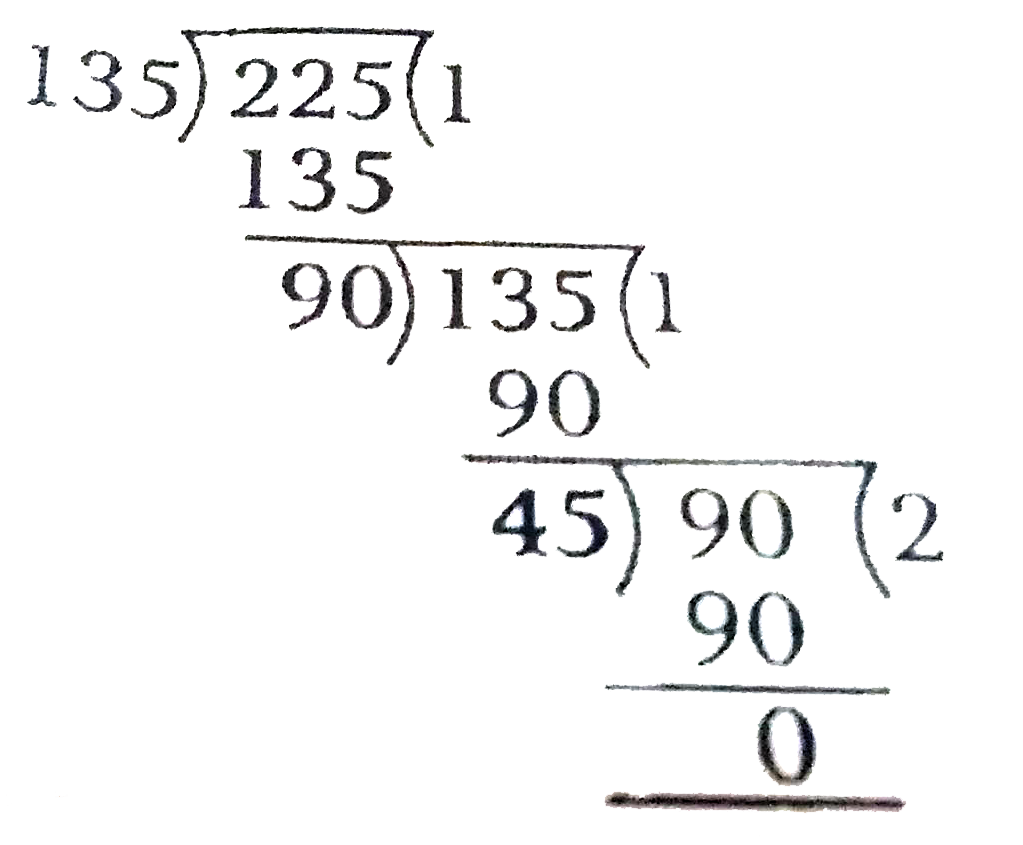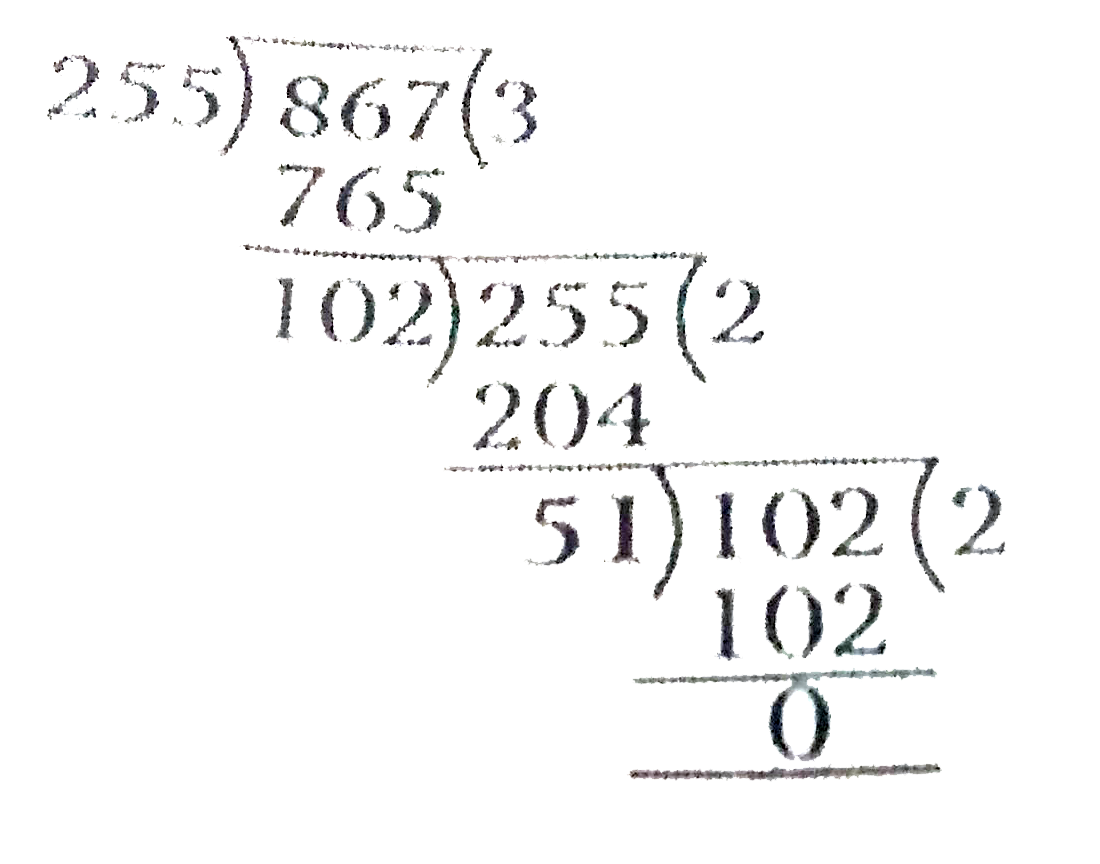Text Solution
Verified by Experts
Topper's Solved these Questions
REAL NUMBERS
NAGEEN PRAKASHAN ENGLISH|Exercise Solved Example|15 VideosREAL NUMBERS
NAGEEN PRAKASHAN ENGLISH|Exercise Problems From NCERT/ Exemplar|11 VideosQUADRATIC EQUATIONS
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Questions|6 VideosSOME APPLICATIONS OF TRIGONOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Long Answer Questions|5 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-REAL NUMBERS-Revision Exercise Long Answer Questions
- Use Euclid's division algorithm to find the HCF of (i) 135 and 2...
Text Solution
|
- Prove that if x and y are odd positive integers, then x^2+y^2 is even ...
Text Solution
|
- about to only mathematics
Text Solution
|
- Prove that if a positive integer is of the form 6q+5 , then it is o...
Text Solution
|
- Prove that the square of any positive integer is of the form 5q ,5q+1,...
Text Solution
|
- Show that the square of an odd positive integer is of the form 8q+1, f...
Text Solution
|