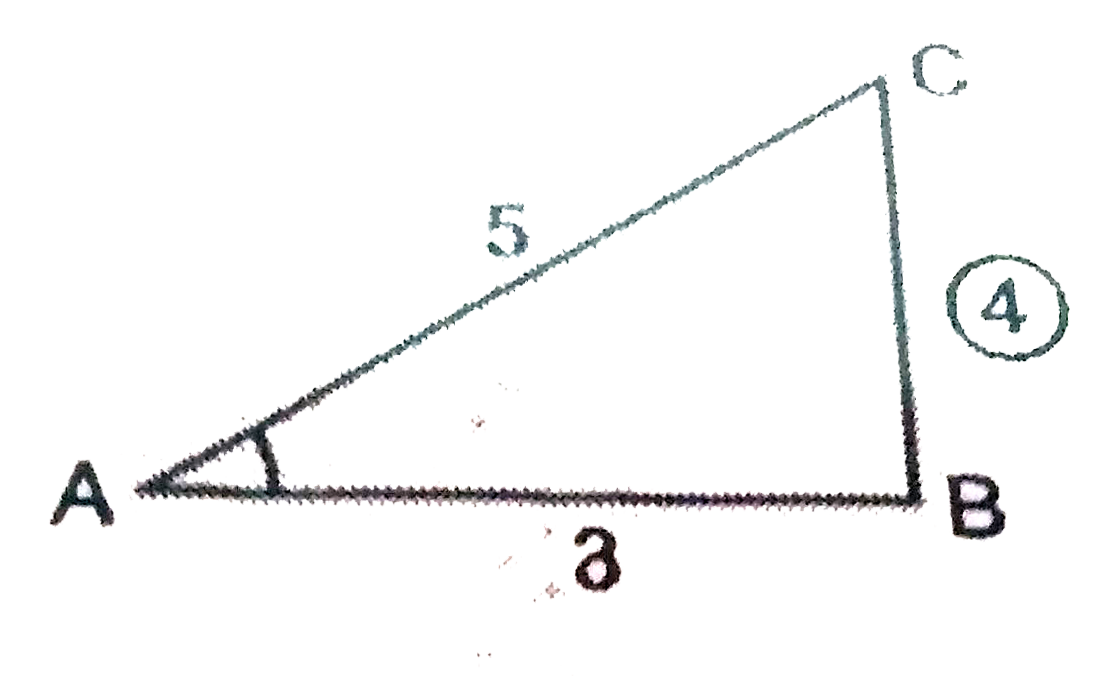
Text Solution
Verified by Experts
Topper's Solved these Questions
QUADRATIC EQUATIONS
NAGEEN PRAKASHAN ENGLISH|Exercise Problems From NCERT /exemplar|17 VideosQUADRATIC EQUATIONS
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 4a|37 VideosPROBABILITY
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Very Short Answer/short Answer Questions|16 VideosREAL NUMBERS
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Questions|5 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-QUADRATIC EQUATIONS-Revision Exercise Long Answer Questions
- In a Delta ABC the value of /A is given by 5 CosA - 3 = 0 then the equ...
Text Solution
|
- Solve the following quadratic equations by factorization method: 1/...
Text Solution
|
- Solve 5^(x+1)+5^(2-x)=5^3+1
Text Solution
|
- find the roots of the following equation by applying the quadratic for...
Text Solution
|
- Solve each of the following quadratic equations: (a)/((x-b))+(b)/((x...
Text Solution
|
- Solve for: 1/(2a+b+2x)=1/(2a)+1/b+1/(2x)
Text Solution
|
- Using quadratic formula, solve the following equation for x: a b x^2+...
Text Solution
|