Text Solution
Verified by Experts
Topper's Solved these Questions
CIRCLES
NAGEEN PRAKASHAN ENGLISH|Exercise Problems From NCERT/exemplar|11 VideosCIRCLES
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise|32 VideosARITHMETIC PROGRESSION
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Question|5 VideosCO-ORDINATE GEOMETRY
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Short Answer Questions|10 Videos
Similar Questions
Explore conceptually related problems
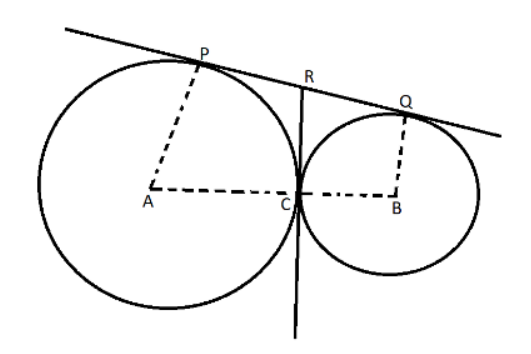
 Hence Proved.
Hence Proved.