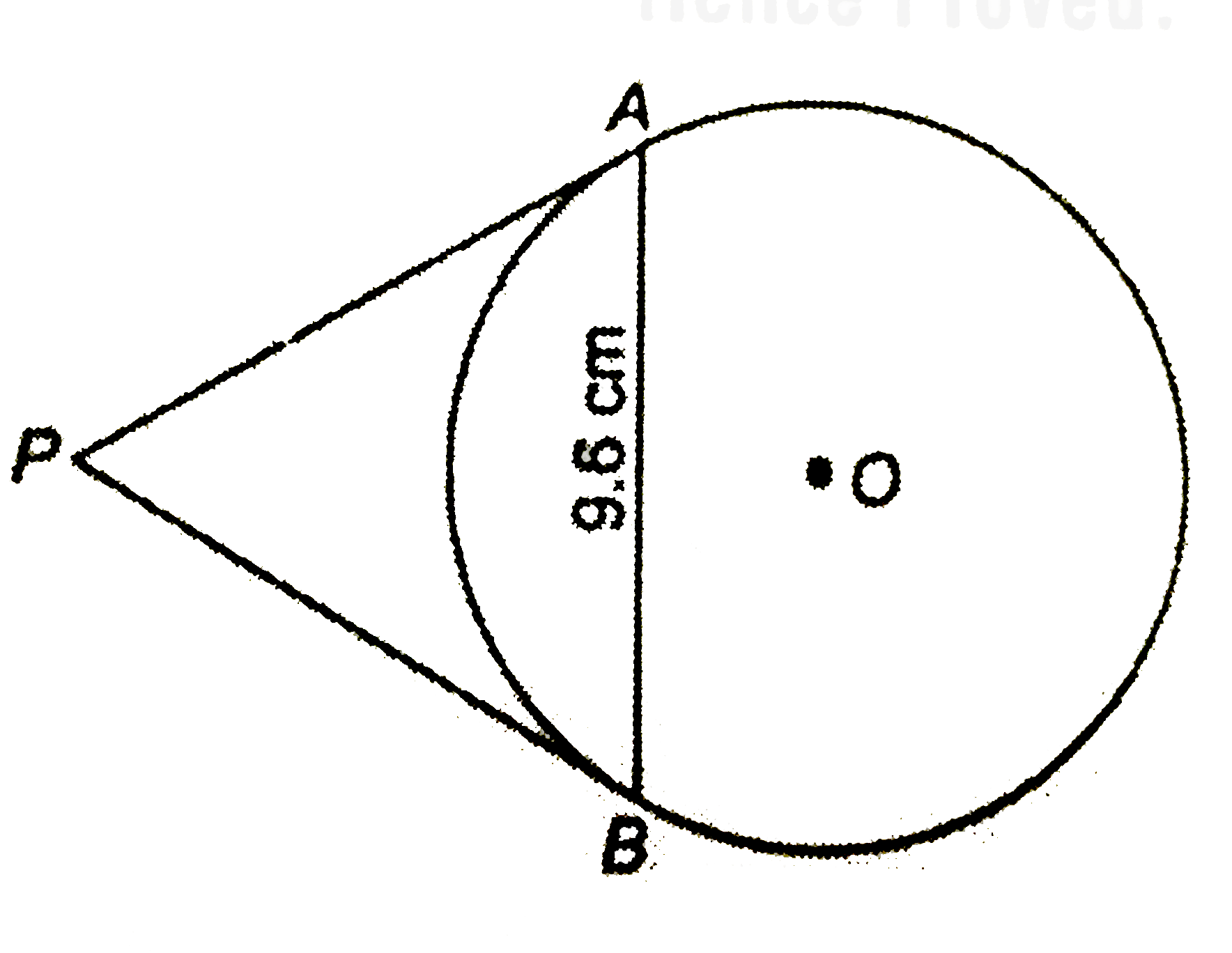
Join OP,OA and OB.
Let `PA = x cm` and `PM = y cm`
In `triangleAPM` and `triangleBPM`
`because" "{{:(PA=PB" ""(length of tangents from an external point are equal)"),(PM=PM" ""(common)"),(angle1=angle2" ""(tangents are equally inclined at the centre)"):}`
`:." "triangleAMP~=triangleBPM" "`(SAS congruency)
`:. " "AM=MB=(9.6)/(2)=4.8 cm" "`(c.p.c.t)
and `anglePMA=anglePMB" "`(c.p.c.t)
But `anglePMA+anglePMB=180^(@)" "`(L.P.A)
`:." "anglePMA=anglePMB=90^(@)`
Now, in right `triangleAMP,`
`x^(2)=y^(2)+(4.8)^(2)" "`(by Pythagoras theorem)
.....(1)
Also, in right `triangleAMO,`
`(4.8)^(2)+OM^(2)=(6)^(2)`
`:." "OM^(2)=36-23.04=12.96`
`:." "OM=sqrt(12.96)=3.6cm`
Now `" "angleOAP=90^(@)" "`(radius through point of contact is `_|_` to the tangent)
In right `triangleAOP,`
`OP^(2)= OA^(2)+AP^(2)`
`implies" "(y+3.6)^(2)=36+x^(2)`
`implies y^(2)+12.96+7.2y=36+y^(2)+(4.8)^(2)" "`[from (1)]
`implies" "7.2y=36+23.04-12.96" "implies" "7.2y=46.08`
`implies" "y=(46.08)/(7.2)=6.4cm`
Put this value of y in equation (1),
`:." "x^(2)=(6.4)^(2)+(4.8)^(2)=40.96+23.04=64`
`:." "x=8cm`
Hence, `x=8 cm` and `y= 6.4 cm`