Home
Class 10
MATHS
The pair of equations y = 0 and y = -7 h...

The pair of equations `y = 0` and `y = -7` has

Text Solution

Verified by Experts

Graphically y = 0 is a straight line which is x - axis and y = - 7 is a straight line parallel to x - axis, 7 units below the origin therefore lines y = 0 and y = - 7 are parallel.
`therefore` They have no solution.
(because solution is the intersection point of both the lines).
Promotional Banner

Topper's Solved these Questions

  • LINEAR EQUATIONS IN TWO VARIABLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 3a|18 Videos

  • LINEAR EQUATIONS IN TWO VARIABLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 3A|8 Videos

  • INTRODUCTION TO TRIGONOMETRY

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Questions|5 Videos

  • POLYNOMIALS

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Questions|4 Videos

Similar Questions

Explore conceptually related problems

The pair of equations x + 2y + 5 = 0 and -3x - 6y + 1 = 0 has

For what value(s) of k, the pair of linear equations -2x + 5y = 0 and kx + 3y = 0 has a non-zero solutions?

Graphically, the pair of equations 6x - 3y+10 = 0 2x - y + 9 = 0 represents two lines which are

Which of the following (x,y) pairs is the solution for the system of equations x + 2y = 4 and -2x + y = 7 ?

The linear equation 2x-5y=7 has

For the pair of equations lambdax + 3y + 7 = 0 and 2x + 6y - 14 = 0 . To have infinitely many solutions, the value of lambda should be 1 . Is the statement true ? Give reasons.

For the pair of equations lambdax + 3y + 7 = 0 and 2x + 6y - 14 = 0 . To have infinitely many solutions, the value of lambda should be 1 . Is the statement true ? Give reasons.

A pair of linear equations which has a unique solution x = 2 and y = -3 is

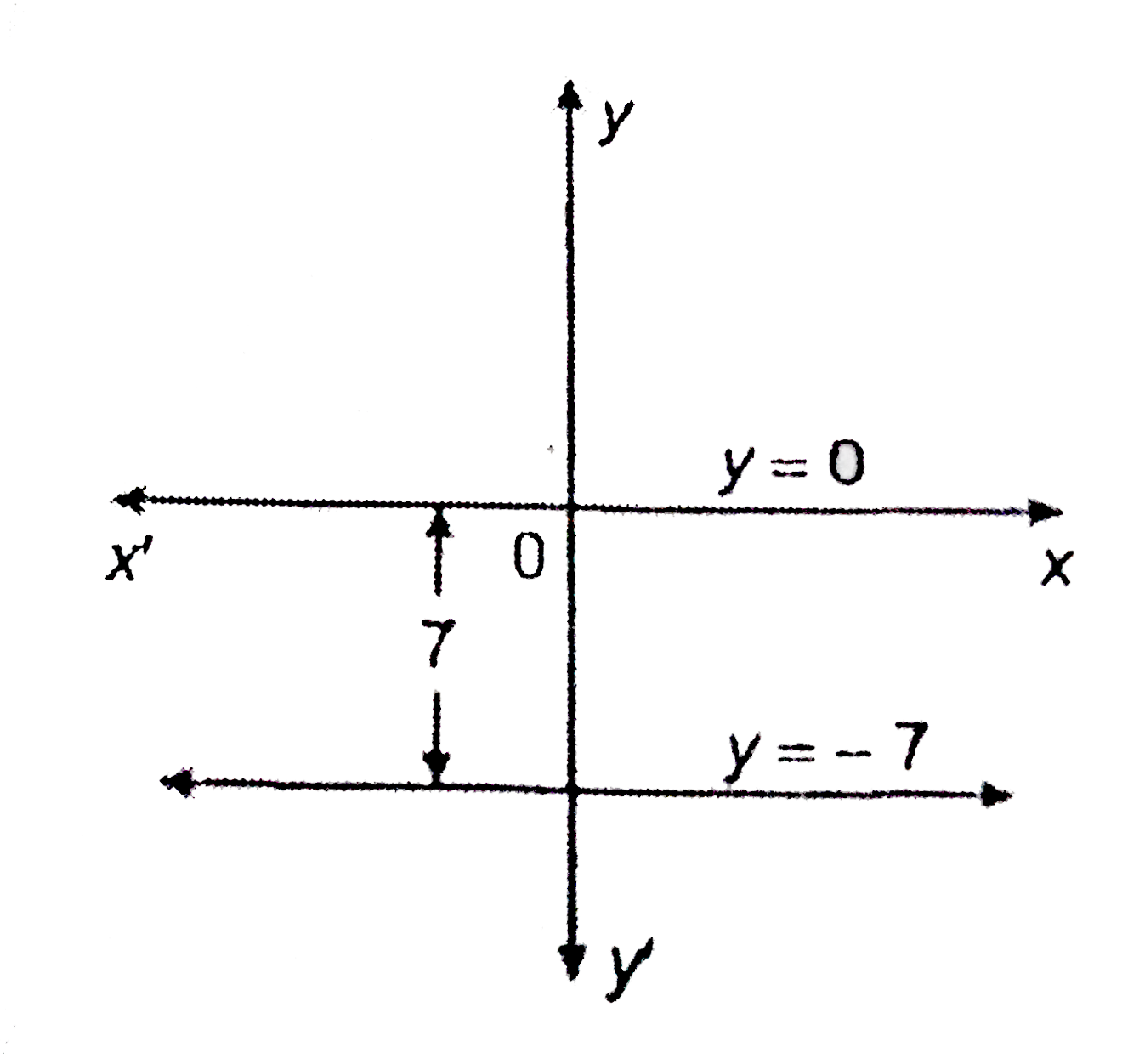
For which values of p does the pair of equations given below has unique solution? 4x+p y+8=0 2x+2y+2=0

If the system of equations x+a y=0,a z+y=0,a n da x+z=0 has infinite solutions, then the value of equation has no solution is -3 b. 1 c. 0 d. 3