Home
Class 9
MATHS
The taxi fare in a city is as follows: ...

The taxi fare in a city is as follows: For the first kilometre, the fare is Rs 8 and for the subsequent distance it is Rs 5 per km. Taking the distance covered as x km and total fare as Rs y, write a linear equation for this information, and draw

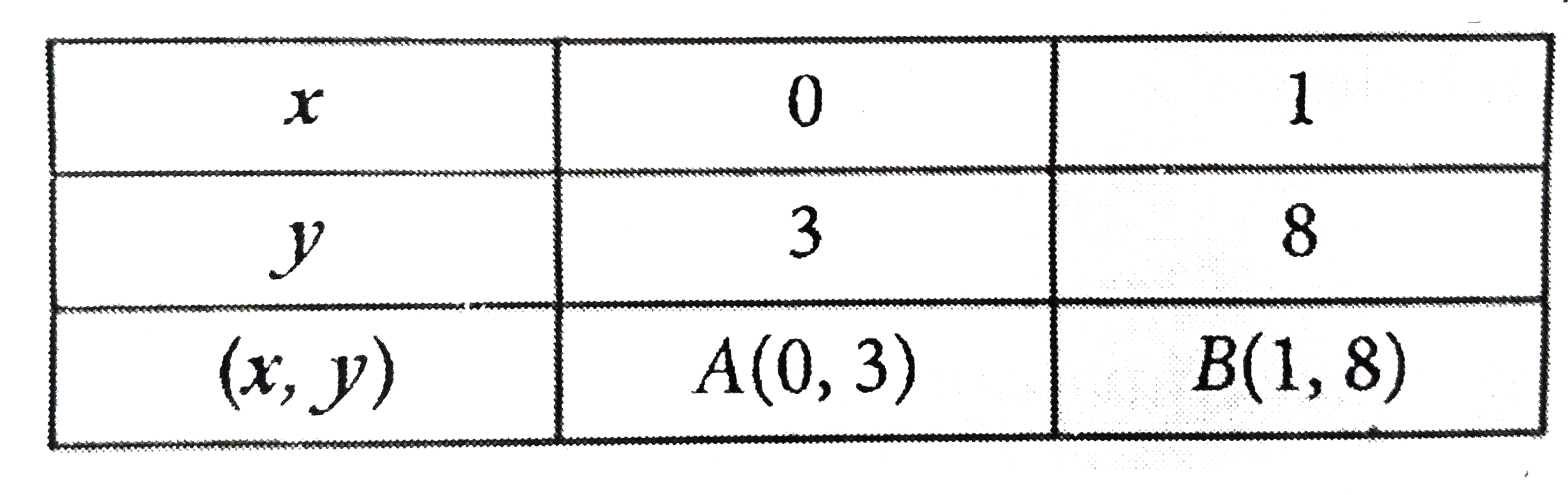
Text Solution

Verified by Experts

Distance covered = x Km =1 + (x-1) Km fare for first kilometre = Rs 8 fare for next (x-1) km=Rs(x-1)xx5=Rs 5(x-1)
According to question total fare =Rs y
8+5(x-1)=y`rArr` 8+5x-5=y `rArr` 5x-y+3=0

Now plot the points A(0,3) and B(1,8) on a graph paper and joining tghem to form a line AB.
Promotional Banner

Topper's Solved these Questions

  • LINEAR EQUATIONS IN TWO VARIABLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise|7 Videos

  • LINEAR EQUATIONS IN TWO VARIABLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise|12 Videos

  • LINEAR EQUATIONS IN TWO VARIABLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise|12 Videos

  • INTRODUCTION TO EUCLID'S GEOMETRY

    NAGEEN PRAKASHAN ENGLISH|Exercise Exercise|8 Videos

  • LINES AND ANGLES

    NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise (long Answer Questions )|6 Videos

Similar Questions

Explore conceptually related problems

A three-wheeler scooter charges 15 for first kilometer and 8 each for every subsequent kilometer. For a distance of x km, an amount of y is paid. Write the equation representing the above information

The taxi charges in a city comprise of a fixed charge together with the charge for the distance covered. For a journey of 10 km the charge paid is Rs 75 and for a journey of 15 km the charge paid is Rs 110. What will a person have to pay for travelling a distance of 25 km?

A lending library has a fixed charge for the first three days and an additional chargefor each day thereafter. Aarushi paid Rs 27 for a book kept for seven days. If fixed charges are Rs x and per day charges are Rs y . Write the linear equation representing the abvoe information.

The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is 315rs and for a journey of 15km, the charge paid is 465rs . What are the fixed charges and the charge per kilometre ? How much does a person have to pay for travelling a distance of 32km ?

The car hire charges in a city comprise of a fixed charges together with the charge for the distance covered. For a journey of 12 km, the charge paid is Rs 89 and for a journey of 20 km, the charge paid is Rs 145. What will a person have to pay for travelling a distance of 30 km?

The taxi fare after each km, when the fare is Rs. 15 for the first km and Rs 8 for each additional km, does not form an AP as the total fare (in Rs.) after each km is 15,8,8,8, … . Is the statement true? Give reasons.

In which of the following situations, does the list of numbers involved make an arithmetic progression, and why? (i) The taxi fare after each km when the fare is Rs 15 for the first km and Rs 8 for each additional km. (ii) The amount of air present in a cylinder when a vacuum pump removes 1/4 of the air remaining in the cylinder at a time. (iii) The cost of digging a well after every metre of digging, when it costs Rs.150 for the first metre and rises by Rs. 50 for each subsequent metre. (iv) The amount of money in the account every year, when 10000 is deposited at compound interest at 8 % per annum.

Ayush starts walking from his house to office . Instead of going to the office directly , he goes to bank first , from there to his daughter 's school and then reaches the office. What is the extra distance travelled by Ayush in reaching his office ? (Assume that all distance covered are in straight lines ). If the house is situated at (2,4) bank at (5,8), school at (13,14) and office at (13,26) and coordinates are in km.

A man at the crossing of two roads x-2y-4=0 and 2x-y=0 , starts walking along the bisector of the acute angle between the roads and after covering a distance 2 km, reaches the bank of a straight river at right angle to its path. Find the equation of the bank and the coordinates of the point where his path meets the bank.

The cost of a notebook is twice the cost of a pen. Write a linear equation in two variables to represent this statement.(Take the cost of a notebook to be Rs x and that of a pen to be Rs y).