Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-CONIC SECTION-Miscellaneous Exercise
- If a parabolic reflector is 20 cm in diameter and 5 cm deep, find its ...
Text Solution
|
- An arc is in the form of a parabola with its axis vertical. The arch i...
Text Solution
|
- The cable of a uniformly loaded suspension bridge hangs in the form...
Text Solution
|
- An arc is in the form of a semi-ellipse. It is 8m wide and 2m high at ...
Text Solution
|
- A rod of length 12 cm moves with its ends always touching the coord...
Text Solution
|
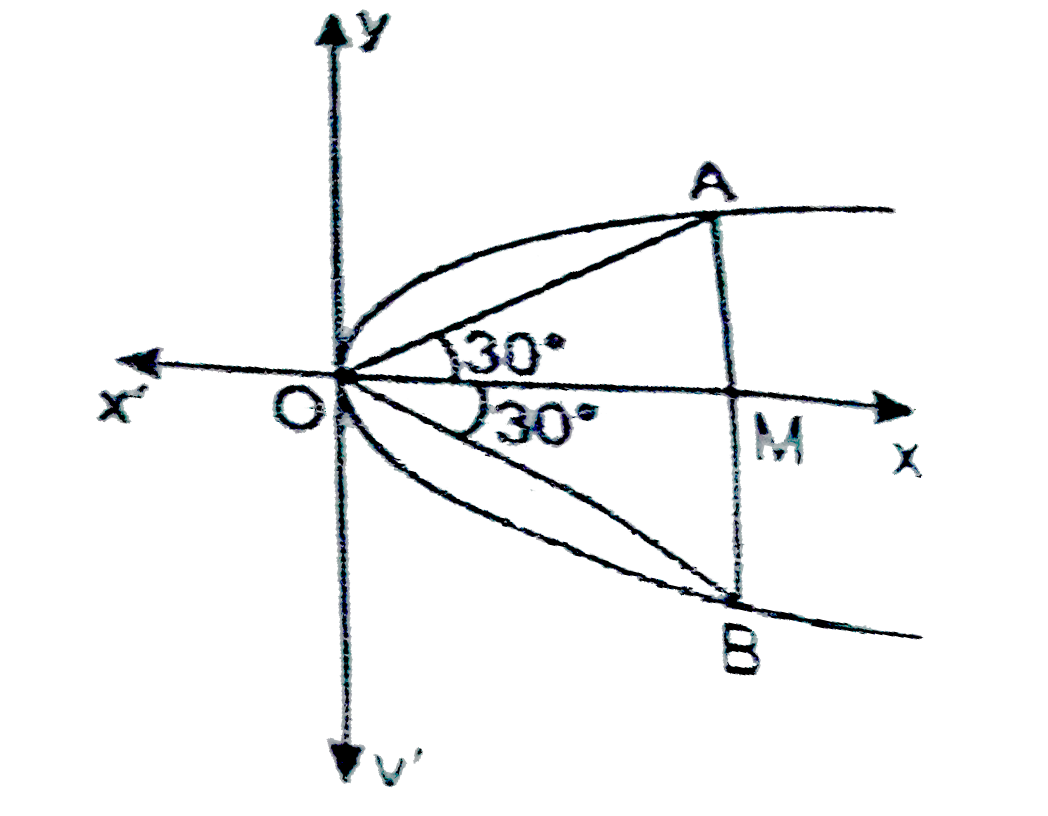
- Find the area of the triangle formed by the lines joining the vertex...
Text Solution
|
- A man running a racecourse notes that the sum of the distances from...
Text Solution
|
- An equilateral triangle is inscribed in the parabola y^(2)=4ax whose v...
Text Solution
|