Text Solution
Verified by Experts
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-VOLUME AND SURFACE AREA OF SOLIDS-Revisions Exercise Long Answer Questions
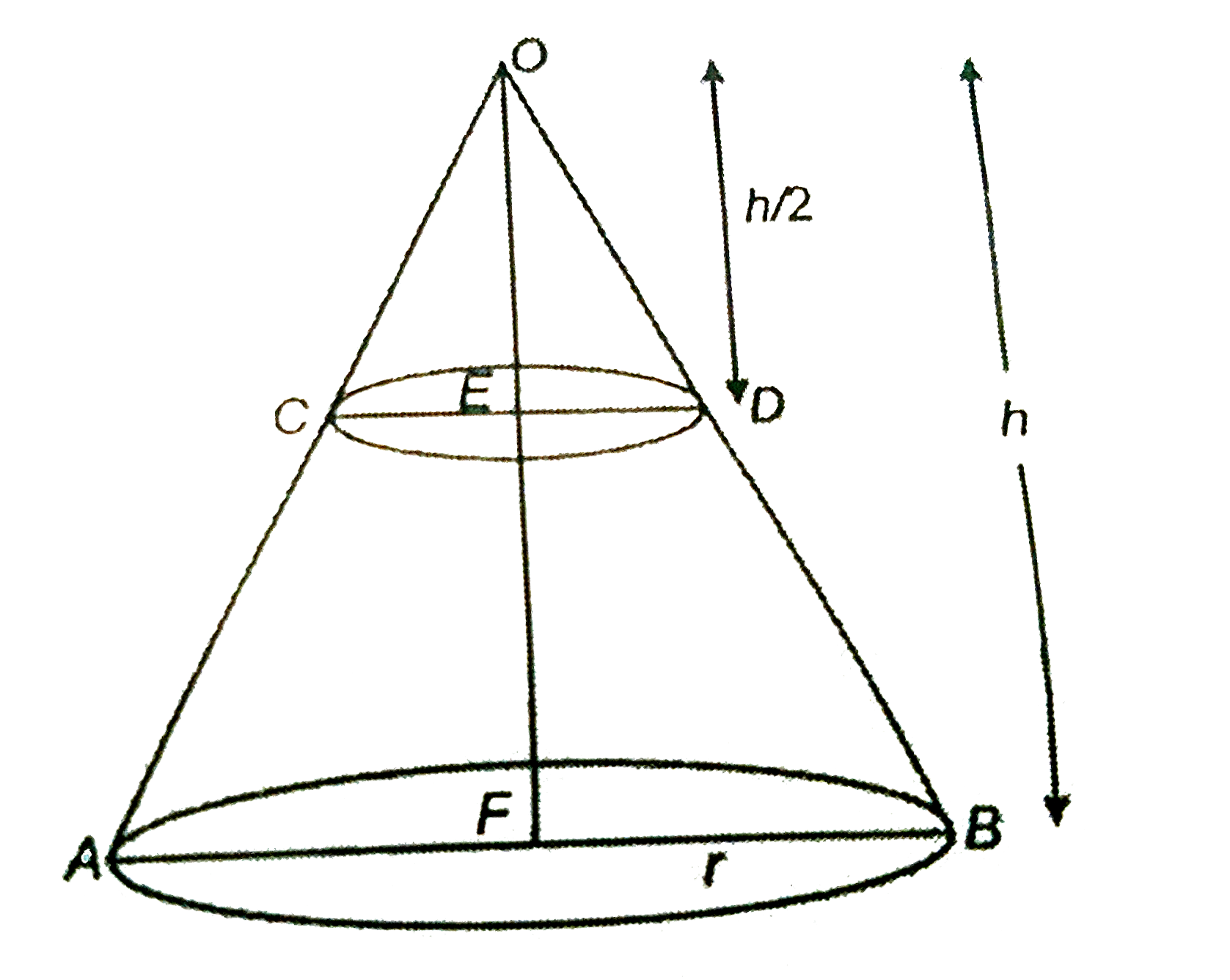
- A cone of radius 8 cm and height 12 cm is divided into two parts by a...
Text Solution
|
- A wooden toy rocket is in the shape of a cone mounted on a cylinder...
Text Solution
|
- Two spheres of same metal weight 1 kg and 7 kg .The radius of the smal...
Text Solution
|
- Water running in a cylindrical pipe of inner diameter 7 cm, is collect...
Text Solution
|
- An open metal bucket is in the shape of a frustum of a cone, mounte...
Text Solution
|
- An oil funnel of tin sheet consists of a cylindrical portion 10 cm ...
Text Solution
|