Text Solution
Verified by Experts
Topper's Solved these Questions
TRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Exercise 6a|24 VideosTRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Eercise 6b|1 VideosTRIANGLES
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Questions|1 VideosSTATISTICS
NAGEEN PRAKASHAN ENGLISH|Exercise Revision Exercise Long Answer Questions|4 VideosVOLUME AND SURFACE AREA OF SOLIDS
NAGEEN PRAKASHAN ENGLISH|Exercise Revisions Exercise Long Answer Questions|5 Videos
Similar Questions
Explore conceptually related problems
NAGEEN PRAKASHAN ENGLISH-TRIANGLES -Problems From NCERT/ Exemplar
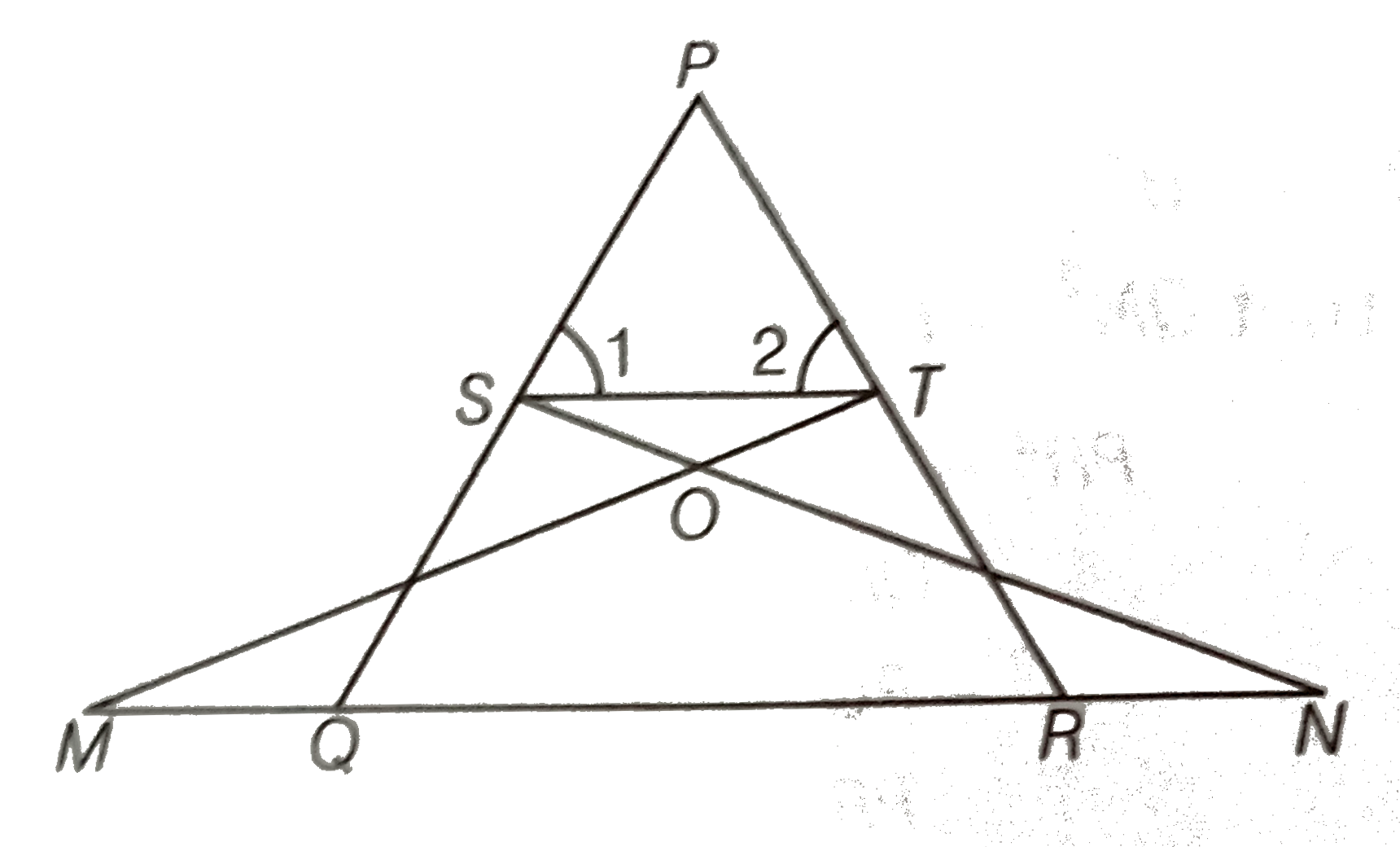
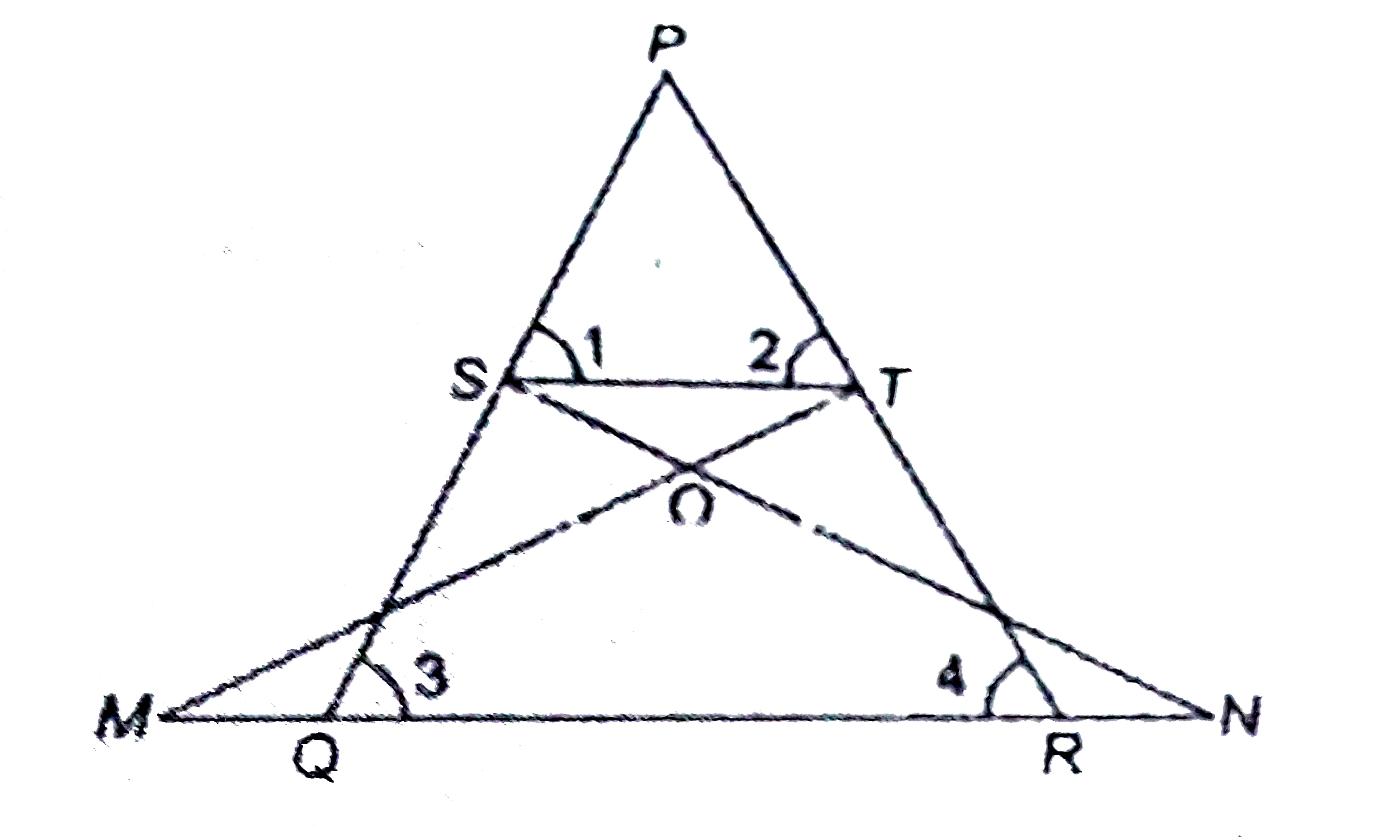
- In figure, if angle1=angle2 and DeltaNSQ=DeltaMTR, then prove that Del...
Text Solution
|
- In figure DE || OQ and DF || OR. Show that EF||QR.
Text Solution
|
- In figure A, B and C are points on OP, OQ and OR respectively such ...
Text Solution
|
- In Figure altitudes AD and CE of A B C intersect each other at the p...
Text Solution
|
- ABCD is a trapezium in which ABabs()DC and P,Q are points on AD and BC...
Text Solution
|
- In figure ABC and DBC are two triangles on the same base BC. If AD in...
Text Solution
|
- Ii DeltaPQR, PDbotQR such that D lies on QR, if PQ=a,PR=b,QD=c and DR=...
Text Solution
|
- In a Delta PQR, N is a point on PR, such that QNbotPR. If PNcdotNR=QN^...
Text Solution
|
- In figure BD and CE intersect each other at the point P. IsDeltaPBC~De...
Text Solution
|
- If in two right triangles, one of the acute angles of one triangle is ...
Text Solution
|
- In P Q R ,\ \ Q M|P R and P R^2-P Q^2=Q R^2 . Prove that Q M^2=P M...
Text Solution
|
- Diagonals of a trapezium PQRS intersect each other at the point 0 ,PQa...
Text Solution
|
- A 5 m long ladder is placed leaning towards a vertical wall such that ...
Text Solution
|
- 14 In Fig. 6.21, PA, QB Rc and SD are all perpendiculars to a line l, ...
Text Solution
|