Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
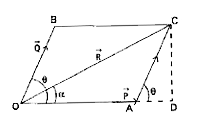
- State parallelogram law of vectors. Derive an expression for the magni...
Text Solution
|
- Asserion: Magnitude of the resultant of two vectors may be less than t...
Text Solution
|
- State parallelogram law of vectors addition .Find analytcallly the mag...
Text Solution
|
- In parallelogram law of vector, the direction of resultant vector is g...
Text Solution
|
- State parallelogram law of vectors . Derive an expression for the magn...
Text Solution
|
- State parallelogram law of vector addition. Find analytically the magn...
Text Solution
|
- According to parallelogram law of vectors the magnitude of resultant o...
Text Solution
|
- Asserion: Magnitude of the resultant of two vectors may be less than t...
Text Solution
|
- A parallelogram law helps to find the magnitude and direction of the r...
Text Solution
|