Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
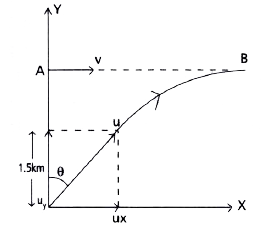
- A fighter plane flying horizontally at an altitude of 1.5 km with spee...
Text Solution
|
- A fightre plane flying horizontally at an altitude oa 1.5 km with spe...
Text Solution
|
- An enemy plane is flying horizontally at an altitude of 2km with a spe...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spe...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spee...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spe...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spee...
Text Solution
|
- A fighter plane flying horizontally at an altitude of 1.5 km with spe...
Text Solution
|
- An enemy plane is flying horizontally at an altitude of 2 km with a sp...
Text Solution
|