Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
VK GLOBAL PUBLICATION-MODEL QUESTION PAPER -2 [UNSOLVED]-SECTION-D
- A motor boat whose speed is 18 km/h in still water takes 1 hour more t...
Text Solution
|
- Prove that in a triangle, if the square of one side is equal to the s...
Text Solution
|
- Draw a circle ofradius 4 cm. Draw two tangents to the circle inclined ...
Text Solution
|
- Draw a circle ofradius 4 cm. Draw two tangents to the circle inclined ...
Text Solution
|
- Draw a circle ofradius 4 cm. Draw two tangents to the circle inclined ...
Text Solution
|
- Draw a circle ofradius 4 cm. Draw two tangents to the circle inclined ...
Text Solution
|
- A fire at a building A is reported on telephone to two fire stations F...
Text Solution
|
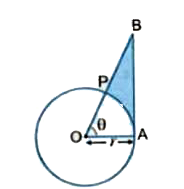
- In Fig. 4, a sector OAP of a circle with centre O, containing angle0. ...
Text Solution
|
- A vessel is in the for1n of an inverted cone. Its height is 8 cm and t...
Text Solution
|
- Find the mean, nmode and median for the following data:
Text Solution
|