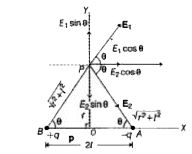
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- An electric dipole of small length lies along X-axis of a coordinates ...
Text Solution
|
- वैधुत द्विध्रुव के कारण अक्षीय रेखा के अनुदिश किसी बिंदु पर विधुत क्षे...
Text Solution
|
- Calculate the electric field due to a dipole on its equatorial plane. ...
Text Solution
|
- Define electric dipole moment. Is it a scalar or a vector ? Derive the...
Text Solution
|
- Deive an expression for the electric field at any point on the equator...
Text Solution
|
- Derive a relation for electric field of an electric dipole at a point ...
Text Solution
|
- Derive an expression for electric potential at any point due to electr...
Text Solution
|
- Derive an expression for the electric field it a point on the equatori...
Text Solution
|
- Derive the expression for the electric field intensity due to an elect...
Text Solution
|