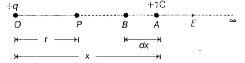
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- Derive an expression for the potential at a distance r from a point ch...
Text Solution
|
- एक बिंदु-आवेश Q से r दूरी पर विधुत-विभव का मान होता है
Text Solution
|
- विद्युत विभव की परिभाषा लिखिए । किसी बिंदु आवेश Q से r दूरी पर स्थित ब...
Text Solution
|
- Derive an expression for the electric potential due to a point charge.
Text Solution
|
- q आवेश r से दूरी पर स्थित किसी बंदु पर वैद्युत विभव का व्यंजक ...........
Text Solution
|
- Determine the potential at a distance r from a point charge +q. How ca...
Text Solution
|
- Derive an expression for gravitational potential energy of a body at a...
Text Solution
|
- Derive an expression for electrostatic potential due to a point charge...
Text Solution
|
- Derive an expression for the electric potential in a electric field of...
Text Solution
|