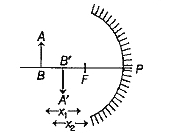Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
- An object is placed at a distance x(1) from the focus of a concave mir...
Text Solution
|
- With a concave mirrorr, an object is placed at a distance x(1) from th...
Text Solution
|
- In a concave mirror experiment, an object is placed at a distance x(1)...
Text Solution
|
- With a concave mirror, an object is placed at a distance x(1) from the...
Text Solution
|
- In a concave mirror, an object is placed at a distance d1 from the foc...
Text Solution
|
- When an small object is placed at a distance x(1) and x(2) from a lens...
Text Solution
|
- In case of thin lens of focal length f an object is placed at a dista...
Text Solution
|
- अवतल दर्पण के किसी प्रयोग में, वस्तु को फोकस से दुरी x(1) पर रखा जाता ...
Text Solution
|
- अवतल दर्पण के एक प्रयोग में वस्तु को दर्पण के फोकस से x(1) दूरी पर रखा...
Text Solution
|