Biot-Savart law: According to this law, the magnetic field dB at the point P due to the small current element of length dI is given by
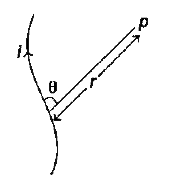
`dB= mu_0 /(4 pi) (idl sin theta)/r^2 Wb//m^2` or tesla
where `mu_0` is a constant and is called permeability of free space.
`mu_0= 4 pi times 10^-7 Wb//A-m`
If the medium is other than air of vaccum, then the magnetic induction is
`dB= (mu_r mu_0)/(4 pi) (i (dl times r))/r^3`
where `mu_r` is the relative permeability of the medium and is a dimensionless quantity.
Magnetic field on the Axis of a Circular current carrying Loop
Let us consider a circular loop of radius a with centre C, Let the plane of the coil be perpendicular to the plane of the paper and current I be flowing in the direction shown. Suppose P is any point on the axis at a direction r from the centre.

Now, consider a current element ldl on top L where current comes out of paper normally. whereas at bottom M enters into the plane paper normally
`because Lp bot dl`
`MP bot dl`
`because LP=MP=sqrt(r^2+a^2)`
The magnetic field at P due to current element ldl.
According to Biot-Savart law
`dB= mu_0/( 4 p). (ldl sin 90^@)/((r^2+a^2))`
where a= radius of circular loop and r= distance of point P from centre along the axis.
The direction of dB is perpendicular to LP and along PQ ,where `PQ bot LP`. Similarly, the same magnitude of magnetic field is obtained due to current element l dl at the bottom and direction is along PQ. where `PQ. bot MP`.
Now, resolving dB due to current element at L and `M.dB cos phi` components balance each other and net magnetic field is given by
`B=int phi dB sin phi`
`=int phi mu_0/(4 pi)((ldl)/(r^2+a^2)).a/sqrt(r^2+a^2)`
`[ because In Delta PCL , sin phi =a/sqrt(r^2+a^2)]`
`=mu_0/(4 pi) (la)/(r^2+a^2)^(3//2) . intphi dl`
`B= mu_0/(4 pi)(la)/(r^2+a^2)^(3//2)(2pi a) or B= (mu_0 la^2)/(2(r^2+a^2)^(3//2)`
FOr N turns , `B = (mu_0Nla^2)/(2(r^2+a^2)^(3//2))`
The direction is along the axis and away from the loop, when current in the coil is in anti clockwise direction.
At the centre of this loop r=0
Putting r=0 in `B=(mu_0N pm a^2)/(2(r^2+a^2)^(3//2))`
`B_(centre)= (mu_0Nl)/(2a)`

