Electric Field The region surrounding a charge or distribution of charge in which its electrical effects can be observed or experienced is called the electric field of the charge or distribution of charge. Electrostatic Potential The electric potential at any point in the region of electric field is defined as the amount of work done in bringing a unit positive test charge (without acceleration) from infinity to that point along any arbitrary. path.
Electrostatic potential (V) = Work done (w) / Charge `(q_0)`
Electric field intensity due to an electric dipole at an equatorial point Consider an electric dipole consisting of two point charges + q and -q separated by a small distance AB = 2l with centre at O and dipole moment, p= q(2l) as . shown in the figure:
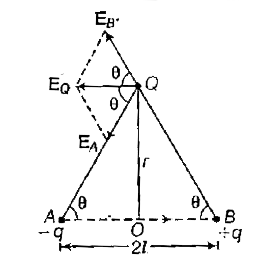
Resultant electric field intensity at the point,Q,
`E_Q = E_A + E_B`
The vectors `E_A` and `E_B` are acting at an angle `2 theta`.
Here, `E_A = (1)/(4pi epsi_0) (q)/((r^2 + l^2))`
`E_B = (1)/(4pi epsi_0 ) (q)/((r^2 + l^2))`
On resolving `E_A` and `E_B` into two rectangular components, the vectors `E_A sin theta` and `E_B sin theta` are equal in magnitude and . opposite to each other and hence cancel out. The vectors `E_A cos theta` and `E_B cos theta` are acting along the same direction and hence add up.
` therefore E_Q = E_A cos theta + E_B cos theta`
` = 2E_A cos theta`
` = (2)/(4pi epsi_0 ) (q)/((r^2 + l^2)). (l)/((r^2 + l^2)^(1//2)) (because cos theta = (l)/((r^2 + l^2)^(1//2)) )`
` = (1)/(4pi epsi_0 ) . (2ql)/((r^2 + l^2)^(3//2)) `
But q x 2l = |p| , the dipole moment,
`E_Q = (1)/(4pi epsi_0 ) . (|p|)/((r^2 + l^2)^(3//2))`
The direction of `E_Q` is along QE || BA, i.e. opposite to AB. In vector form, we can rewrite as
`E_Q = (-p)/(4pi epsi_0 (r^2 + l^2 )^(3//2))`
Obviously, `E_Q` is in a direction opposite to the direction of p. If the dipole is short, i.e. 2l << r, then
`E_Q = (1)/(4pi epsi_0 ) . (|p|)/(r^3)`
