Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
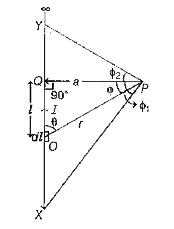
- State Biot-Savart.s law. Derive an expression for magnetic field at a ...
Text Solution
|
- Derive an expression for magnetic field strength B at a point P due to...
Text Solution
|
- Using Ampere's circuital law, obtain an expression for the magnetic in...
Text Solution
|
- Using Gauss’ law, derive an expression for the electric field at a poi...
Text Solution
|
- How does the magnetic field at a point near a long straight current-c...
Text Solution
|
- The magnetic field developed at a point near a straight current carryi...
Text Solution
|
- State Ampere's circuital law . Using it, derive the expression for mag...
Text Solution
|
- The magnetic field near the centre of an infinite long straight curren...
Text Solution
|
- State Ampere's circuital law. By using it derive an expression for mag...
Text Solution
|