Home
Class 10
MATHS
Prove that the tangent drawn at the ends...

Prove that the tangent drawn at the ends of chord of a circle make equal angle with the chord.

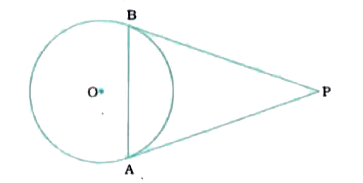
Text Solution

Verified by Experts

The correct Answer is:
`anglePAB=anglePBA`
Promotional Banner

Topper's Solved these Questions

  • CIRCLE

    KUMAR PRAKASHAN|Exercise Textual Examples |3 Videos

  • CIRCLE

    KUMAR PRAKASHAN|Exercise Test Your Skills|12 Videos

  • ARITHMETIC PROGRESSION

    KUMAR PRAKASHAN|Exercise OBJECTIVE QUESTIONS|1 Videos

  • CONSTRUCTIONS

    KUMAR PRAKASHAN|Exercise OBJECTIVE QUESTIONS|25 Videos

Similar Questions

Explore conceptually related problems

Prove that tangent drawn at the ends of a diameter of a circle are parallel.

If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.

Prove that the lengths of tangents drawn from an external point to a circle are equal.

Fill in the blanks Prove that the tangents to a circle at the end points of a diameter are parallel.

Recall that two circles are congruent if they have the same radii. Proe that equal chords of congruent circles subtend equal angles at their centres.

If two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection, prove that the chords are equal.

If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to correspondig segments of the other chord.

Prove that if chords f congruent circles subtend equal angles at their centres, then the chords are equal.

State true or false . The longest of all chords of a circle is called a diameter.