Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-AREAS RELATED TO CIRCLES-Other Important Examples
- Find the diameter of the circle whose area is equal to the sum of the ...
Text Solution
|
- The diameters of the front and the rear wheels of a tractor are 80cm a...
Text Solution
|
- The difference between the radii of the bigger circle and the smaller ...
Text Solution
|
- Find the differnce of the areas of a minor sector of angle 120^(@) and...
Text Solution
|
- A piece of wire 20 cm long is bent into the form of an arc of a circle...
Text Solution
|
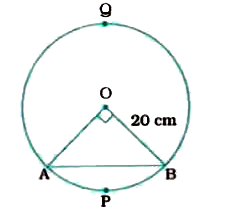
- A chord of a circle of radius 20 cm subtends an angle of 90^(@) at the...
Text Solution
|
- In the given figure, find the area of the shaded region. (Use pi = 3.1...
Text Solution
|
- An archery target has three regions formed by three concentric circles...
Text Solution
|
- In the given figure, ABCD is a trapezium with AB||DC, AB = 18 cm, DC =...
Text Solution
|