Text Solution
Verified by Experts
The correct Answer is:
Topper's Solved these Questions
AREAS RELATED TO CIRCLES
KUMAR PRAKASHAN|Exercise Practice Thoroughly|8 VideosAREAS RELATED TO CIRCLES
KUMAR PRAKASHAN|Exercise Objective Questions|25 VideosAREAS RELATED TO CIRCLES
KUMAR PRAKASHAN|Exercise Exercise 12.3|16 VideosARITHMETIC PROGRESSION
KUMAR PRAKASHAN|Exercise OBJECTIVE QUESTIONS|1 Videos
Similar Questions
Explore conceptually related problems
KUMAR PRAKASHAN-AREAS RELATED TO CIRCLES-Test Your Skills
- The circumference of a circle exceeds its diameter by 30 cm. Find the ...
Text Solution
|
- The area of a circular playground is 22,176 m^(2). Find the cost of fa...
Text Solution
|
- The area enclosed between two concentric circles is 770 cm^(2). If the...
Text Solution
|
- The wheels of a motorcycle are of radius 35 cm. How many revolutions p...
Text Solution
|
- A path of width 3.5m runs around the curved boundary of a semicircular...
Text Solution
|
- Find the area of the minor segment of a circle of radius 14 cm. When t...
Text Solution
|
- Find the area of a sector of a circle of radius 28 cm and central angl...
Text Solution
|
- A cow is tied with a rope of length 14 m at the corner of a rectangula...
Text Solution
|
- A chord of a circle of radius 14 cm makes a right angle at the centre....
Text Solution
|
- A chord of a circle of radius 10 cm subtends a right angle at the cent...
Text Solution
|
- In the given figure, ABC is a right triangle, right angled at A. AB = ...
Text Solution
|
- In the given figure, PQRS is a diameter of circle with radius 6cm, suc...
Text Solution
|
- A paper is in the form of a rectangle ABCD in which AB = 18 cm and BC ...
Text Solution
|
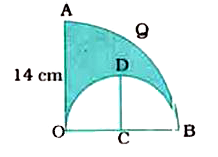
- OAQB is a quadrant of a circle with centre O and radius 14 cm. A semic...
Text Solution
|
- What is the area of an equilateral triangle inscribed in a circle of r...
Text Solution
|