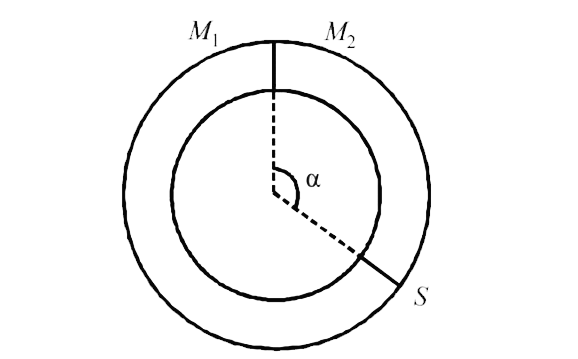
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- A ring shaped tube contain two ideal gases with equal masses and mola...
Text Solution
|
- A ring shaped tube contain two ideal gases with equal masses and relat...
Text Solution
|
- A conducting piston separates a cylindrical tube into two compartments...
Text Solution
|
- As isolated box, equally partitioned contains two ideal gases A and B ...
Text Solution
|
- A ring - shaped tube contains two ideal gases with equal masses and re...
Text Solution
|
- एक वलयाकार नाली में समान द्रव्यमान की दो आदर्श गैसें भरी है, जिनके अणु...
Text Solution
|
- If two masses m1 and m2 (m1 gt m2) tied to string moving over a fricti...
Text Solution
|
- The RMS velocities of two gases at the same temperature are u1 and u2 ...
Text Solution
|
- A body of mass m(1) moving with uniform velocity of 40 m/s collides w...
Text Solution
|