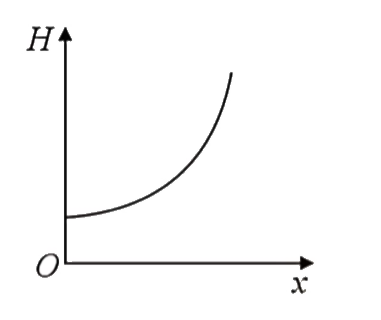
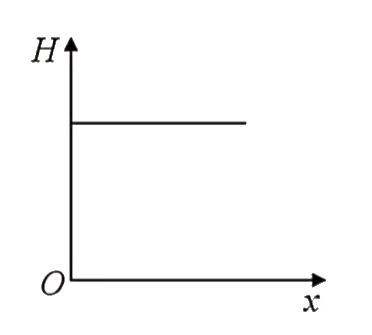
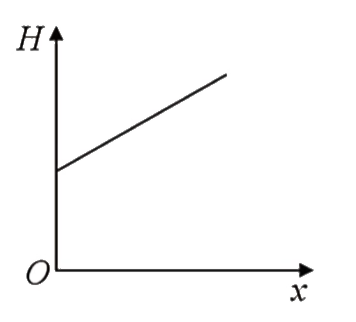
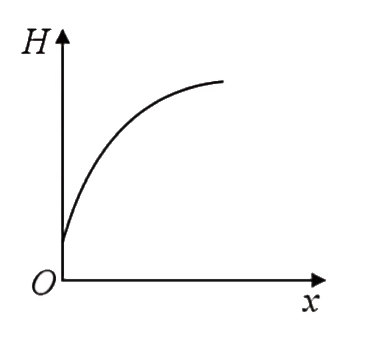
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Radius of a conductor increases uniformly from left end to right end a...
Text Solution
|
- Shown below are the black body radiation curves at temperature T(1) an...
Text Solution
|
- A rod of unifrom cross section is heated at temperature t(0) at a poin...
Text Solution
|
- A cylindrical rod of length l, thermal conductivity k and area of cros...
Text Solution
|
- In the frame shown in figure made up of metallic rods of identical siz...
Text Solution
|
- The V - i graph for a conductor at temperature T(1) and T(2) are as sh...
Text Solution
|
- A thin piece of thermal conductor of constant thermal conductivity ins...
Text Solution
|
- Two bars of same length and same cross-sectional area but of different...
Text Solution
|
- चित्र में विभवांतर V और धारा I के बीच किसी चालक के दो ताप T(1)और ...
Text Solution
|