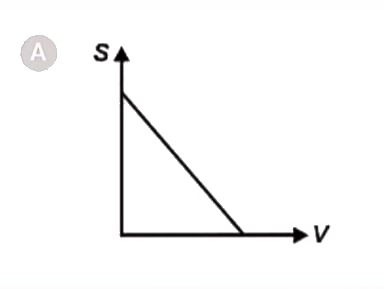
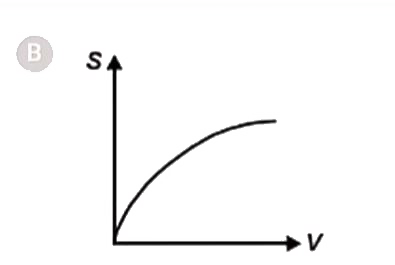
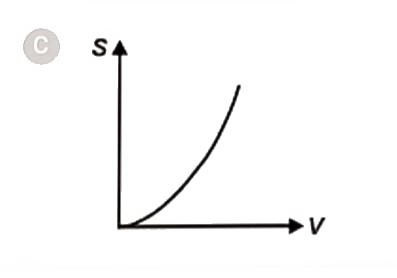
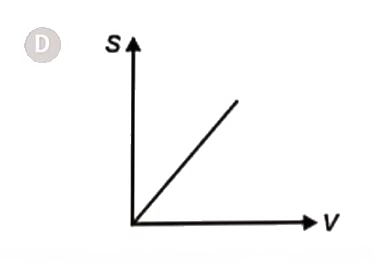
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- The displacement (s)- velocity ( v ) graph of a particle if it starts ...
Text Solution
|
- An object is moving with a uniform acceleration which is parallel to i...
Text Solution
|
- A particle starts from rest with uniform acceleration a. Its velocity ...
Text Solution
|
- For an object starting from rest with uniform acceleration which of th...
Text Solution
|
- एक पिण्ड एकसमान त्वरण से विरामावस्था से चलता है। सिद्ध कीजिये की s तथा...
Text Solution
|
- The displacement (s)- velocity ( v ) graph of a particle if it starts ...
Text Solution
|
- A particle starts from rest and moves with constant acceleration. Then...
Text Solution
|
- एक कण नियत त्वरण से गतिशील है, जिसकी दिशा कण की गति की तात्क्षणिक दिशा...
Text Solution
|
- An object is moving with a uniform acceleration which is parallel to i...
Text Solution
|