A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
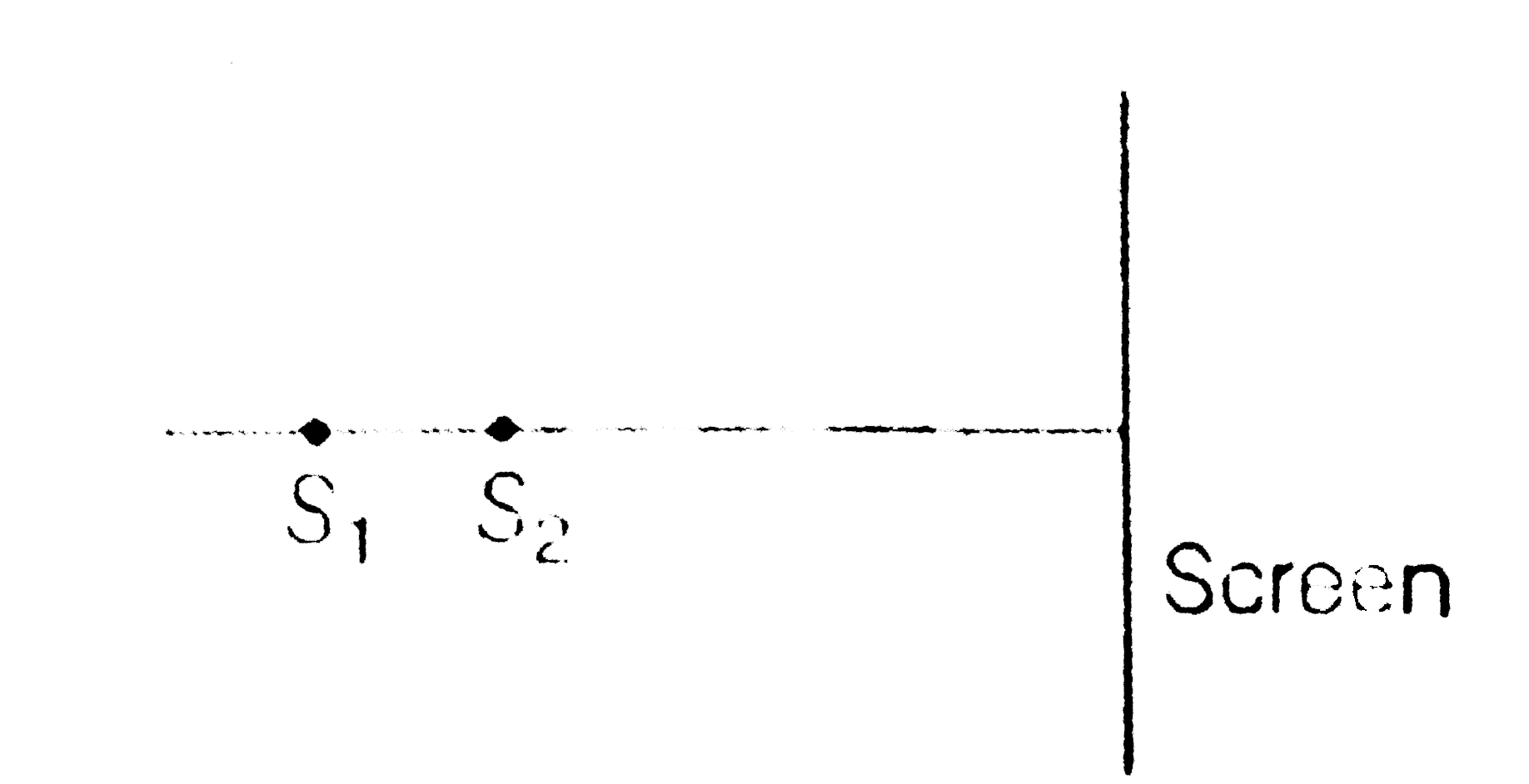
- Two coherent point sources S(1) and S(2) separted by a small distance ...
Text Solution
|
- While conduction the Young's double slit experiment, a student replace...
Text Solution
|
- Two coherent point sources S1 and S2 are separated by a small distance...
Text Solution
|
- Three coherent point sources S(1),S(2) and S(3) are placed on a line p...
Text Solution
|
- दो कला सम्बद्ध बिन्दु स्त्रोत S(1) व S(2) अल्प दूरी d से पृथक्कृत ह...
Text Solution
|
- दो कला संबद्ध स्त्रोत S(1) व S(2) एक-दूसरे से d दुरी पर विभक्त है - ...
Text Solution
|
- In Young's double slit experiment, an interference pattern is obtained...
Text Solution
|
- Two coherent point sources S1 and S2 are separated by a small distance...
Text Solution
|
- Two coherent point sources S(1) and S(2) are separated by a small dist...
Text Solution
|