A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
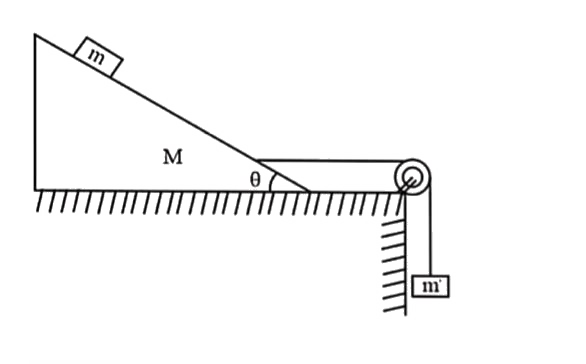
- A hanging block of mass m' prevents the smaller block of mass m from s...
Text Solution
|
- Find the mass M of the hanging block in figure which will prevent the ...
Text Solution
|
- A block of mass m is placed on a triangular block of mass M(M = 2m) , ...
Text Solution
|
- Assuming all the surfaces to be smooth, find the acceleration of the t...
Text Solution
|
- Find the mass (in kg) of the hanging block which will prevent the smal...
Text Solution
|
- Find the mass of the hanging block in which will prevent the smaller b...
Text Solution
|
- In the arrangement shown in figure , there is friction between the bl...
Text Solution
|
- A block of mass M is placed on a horizontal surface. It is tied with a...
Text Solution
|
- A hanging block of mass m' prevents the smaller block of mass m from s...
Text Solution
|