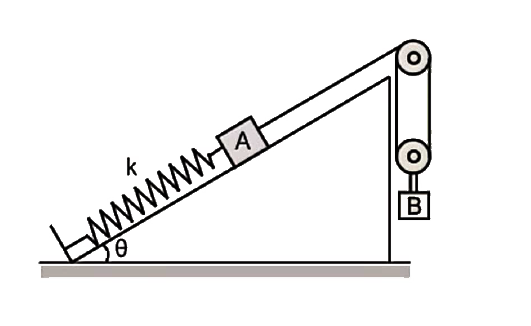
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Friction is absent everywhere and the threads, spring and pulleys are ...
Text Solution
|
- Calculate the angular frequency of the system shown in fingure. Fricti...
Text Solution
|
- A pulley fixed to the ceiling carried a thread with bodies of masses m...
Text Solution
|
- In the system shown in figure m(B)=4kg , and m(A)=2kg . The pulleys ar...
Text Solution
|
- In arrangement shown below, the thread pulley and spring are all massl...
Text Solution
|
- A pulley fixed to the ceiling carries a thread with bodies of masses ...
Text Solution
|
- Two mass m(1) and m(2) are suspended from a massless spring of force c...
Text Solution
|
- Friction is absent everywhere and the threads, spring and pulleys are ...
Text Solution
|
- Two masses m(1) and m(2) are suspended together by a massless spring o...
Text Solution
|