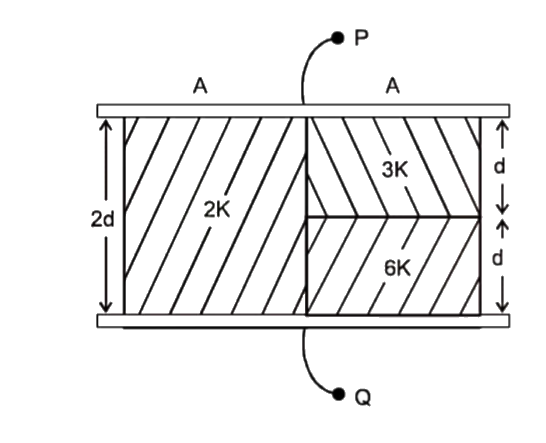
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Three different types of dielectric slabs have been arranged between t...
Text Solution
|
- The space between the plates of a parallel plate capacitor of capacit...
Text Solution
|
- Find the capacitances of the capacitance of the capacitors shown In f...
Text Solution
|
- Three different types of dielectric slabs have been arranged between t...
Text Solution
|
- A parallel plate capacitor with air as the dielectric has capacitance ...
Text Solution
|
- A dielectric slab is placed between the plates of a parallel plate cap...
Text Solution
|
- The space between the plates of a parallel plate capacitor of capacit...
Text Solution
|
- Find the capacitances of the capacitance of the capacitors shown In f...
Text Solution
|
- Derive an expression for capacitance of a parallel plate capacitor.
Text Solution
|