Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
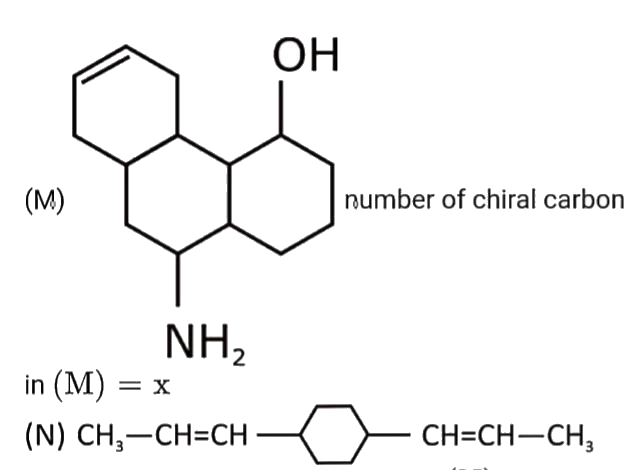
- in (M)=x (Number of Geometrial isomers in (N)=y). The value of (y...
Text Solution
|
- If(cos(x-y))/(cos(x+y)=(m)/(n))8. If cos(X-Y=m then write the value of...
Text Solution
|
- Find the maximum value of x^(m)y^(n),m,n>0 such that x+y=a.
Text Solution
|
- In the monochlorination of 3-methylpentan, let x be the number of pair...
Text Solution
|
- If (x+y)^(m+n)=x^(m)y^(n), then the value of (dy)/(dx) is -
Text Solution
|
- If x^(m) y^(n) =2(x+y)^(m+n), the value of (dy)/(dx) is
Text Solution
|
- in (M)=x (Number of Geometrial isomers in (N)=y). The value of (y)/(x)...
Text Solution
|
- If x, y, k, m, n are positive and x + y = k, then find the maximum val...
Text Solution
|
- यदि x^(m) y^(n) = 2 (x + y)^(m+n), तो dy/dx का मान है :
Text Solution
|