A
B
C
D
Text Solution
Verified by Experts
Similar Questions
Explore conceptually related problems
Recommended Questions
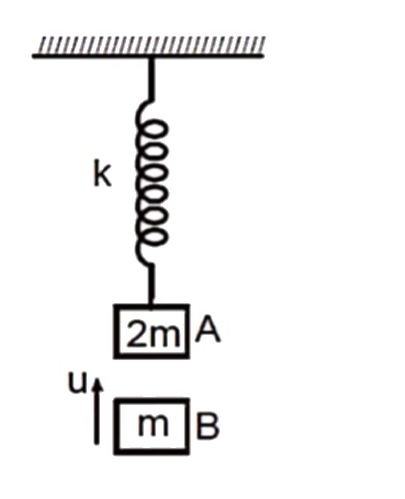
- A block A of mass 2m is hanging from a vertical massless spring of spr...
Text Solution
|
- A block of mass m is connected to another block of mass M by a spring ...
Text Solution
|
- Two blocks of masses 3kg block is attached to a spring with a force co...
Text Solution
|
- Block A is hanging from vertical spring of spring constant K and is re...
Text Solution
|
- Two springs are in a series combination and are attached to a block of...
Text Solution
|
- A system consists of block A and B each of mass m connected by a light...
Text Solution
|
- A block of mass m is connected to another .block of mass M by a massle...
Text Solution
|
- A block of mass 'm' is connected to another block of mass 'M' by a spr...
Text Solution
|
- A block A of mass 2m is hanging from a vertical massless spring of spr...
Text Solution
|