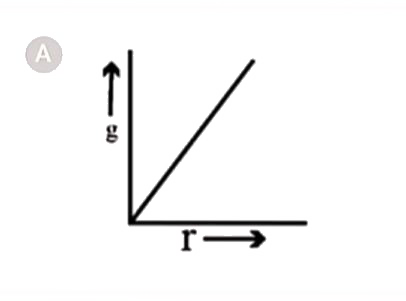
A
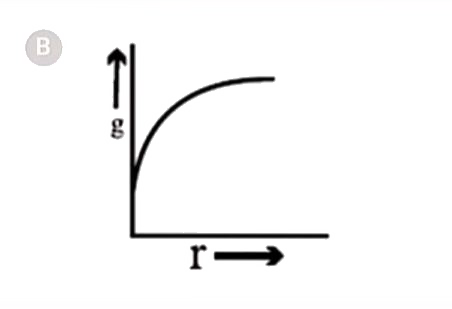
B
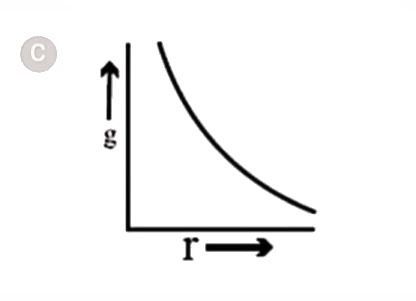
C
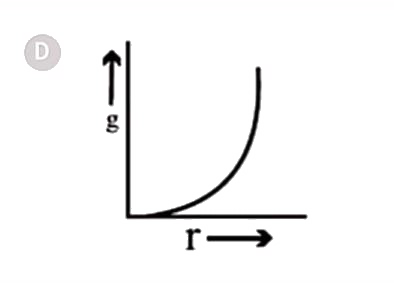
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- If the density of a planet is constant, then the curve between value o...
Text Solution
|
- A planet has twice the density of earth but the acceleration due to gr...
Text Solution
|
- If the radius of a planet is R and its density is rho , the escape vel...
Text Solution
|
- If different planets have the same density but diferent radii then the...
Text Solution
|
- If the density of a planet is constant, then the curve between value o...
Text Solution
|
- यदि किसी ग्रह की त्रिज्या R तथा घनत्व rho हो तो उसके पृष्ठ से पलायन वे...
Text Solution
|
- If a planet gets inflated, keeping its density constant, then g will i...
Text Solution
|
- एक नये खोज किये गये ग्रह का घनत्व पृथ्वी से दोगुना है व इसकी सतह का गु...
Text Solution
|
- A planet has twice the density of earth but the acceleration due to gr...
Text Solution
|