A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
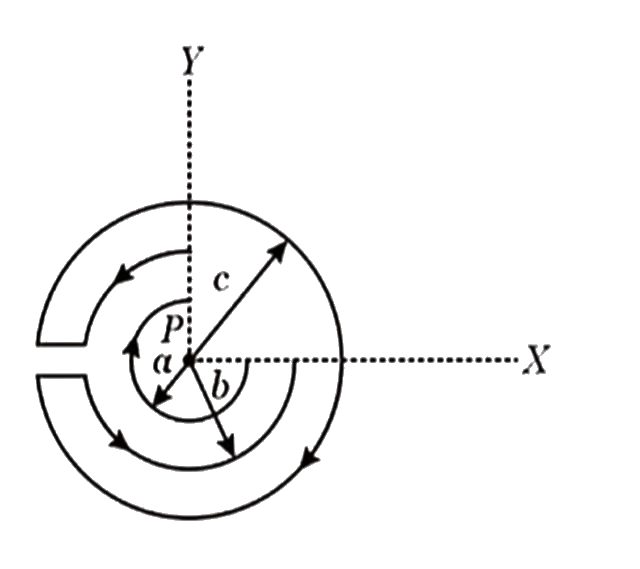
- For c=2a and c lt b lt c, the magnetic field at the point P will be ze...
Text Solution
|
- For c=2a if, the magnetic field at point P will be zero when
Text Solution
|
- Assertion: A gas can be liquefied at T=T(c ) and P lt P(c) Reason: A g...
Text Solution
|
- If a lt b lt c lt d and a , b , c , d are non-zero integers , the me...
Text Solution
|
- If a gt b, " then " (a)/(c) lt (b)/(c) for all a, b and c in R, where ...
Text Solution
|
- If a , b, c, d are non-zero integers such that a lt b lt c lt d and m...
Text Solution
|
- For c=2a and c lt b lt c , the magnetic field at the point P will be z...
Text Solution
|
- If a lt 0, b gt 0 and c lt 0, then the point P(a, b, -c) lies in the ...
Text Solution
|
- For c = 2 a and a lt b lt c , the magnetic field at the point P will ...
Text Solution
|