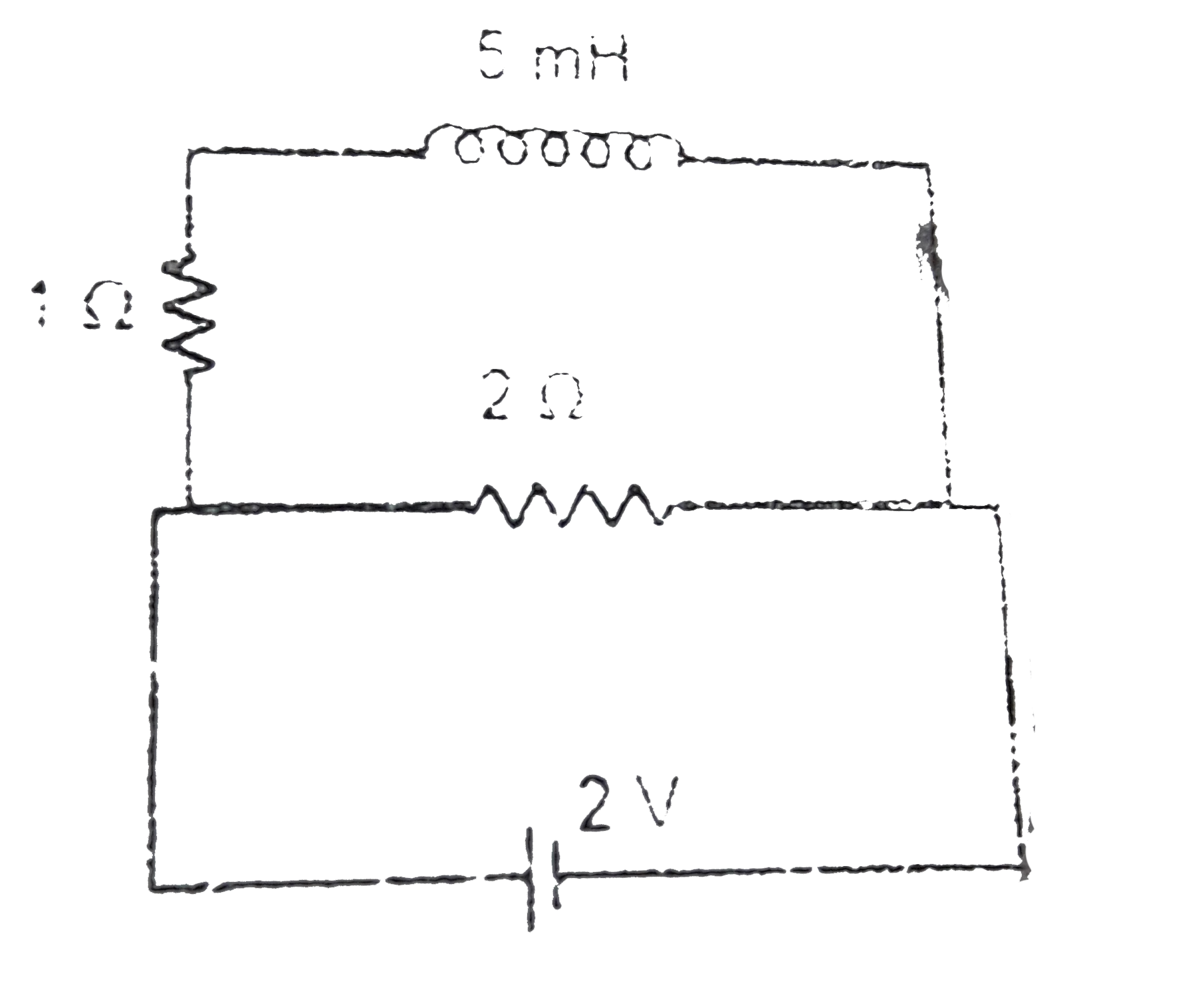
A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- When induced emf in inductor coil is 50% of its maximum value then sto...
Text Solution
|
- An inductor coil stores U energy when i current is passed through it a...
Text Solution
|
- In an induction coil with resistance, the induced emf will be maximum ...
Text Solution
|
- When induced emf in inductor coil is 50% of its maximum value then sto...
Text Solution
|
- Define self-inductance of a coil. Obtain the expression for the energy...
Text Solution
|
- A coil of 10^(-2) H inductance carries a current I = 2sin (100t) A . W...
Text Solution
|
- Define self-inductance of a coil. Obtain the expression for the energy...
Text Solution
|
- The magnetic field at a point inside a 2.0 mH inductor coil becomes 0...
Text Solution
|
- Energy stored in an inductor is given by?
Text Solution
|