A
B
C
D
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
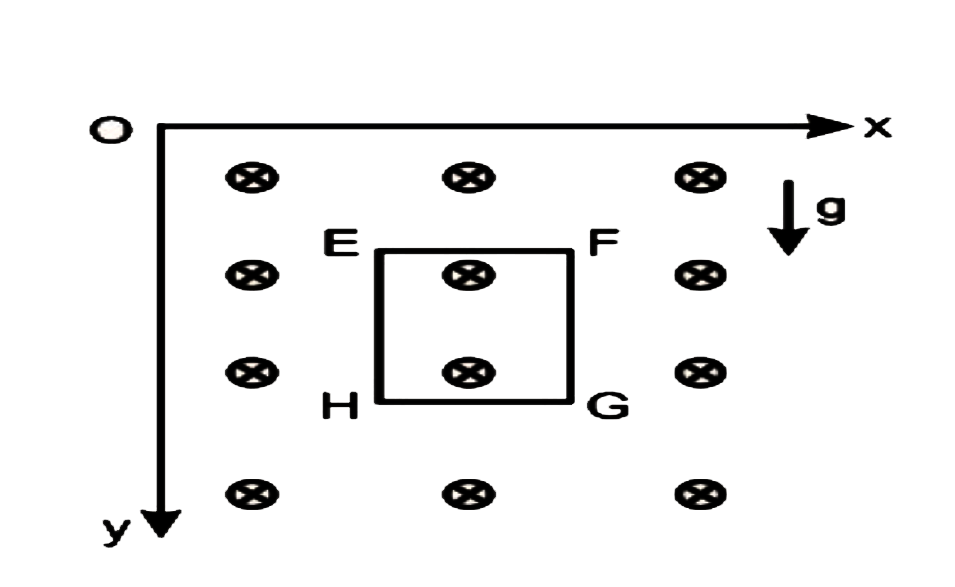
- A square loop EFGH of side a, mass m and total resistance R is falling...
Text Solution
|
- A magnetic field B = B(0) (y//a)(hat)k is into the paper in the +z dir...
Text Solution
|
- A square loop of edge a has N turns and a total resistance R . The loo...
Text Solution
|
- A square loop of side L, resistance R placed in a uniform magnetic fie...
Text Solution
|
- A square loop of sides 10 cm carries a current of 10 A.A uniform magne...
Text Solution
|
- A triangle loop as shown in the figure is started to being pulled out ...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|
- एक चुंबकीय क्षेत्र vec(B) = ((B(0)y)/(a))hatk कागज के तल के लंबवत अं...
Text Solution
|