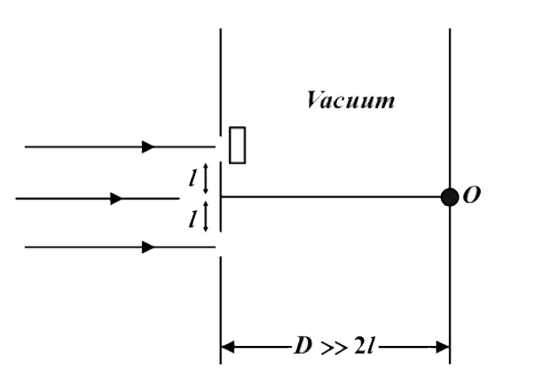
Text Solution
Verified by Experts
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- In young's double-slit experiment, both the slits produce equal intens...
Text Solution
|
- In YDSE, both slits produce equal intensities on the screen. A 100% tr...
Text Solution
|
- The slits in a double-slit interference experiment are illuminated by ...
Text Solution
|
- The maximum intensity in Young's double slit experiment is I(0) . What...
Text Solution
|
- A thin glass plate of thickness t and refractive index mu is inserted ...
Text Solution
|
- In Young's double slit experiment, the distance between the two slits ...
Text Solution
|
- In young's double-slit experiment, both the slits produce equal intens...
Text Solution
|
- Young's double slit experiment is performed with monochromatic light. ...
Text Solution
|
- A thin glass plate of thickness t(=lambda//3,lambda being the waveleng...
Text Solution
|