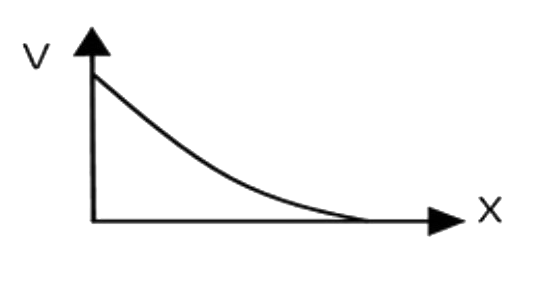
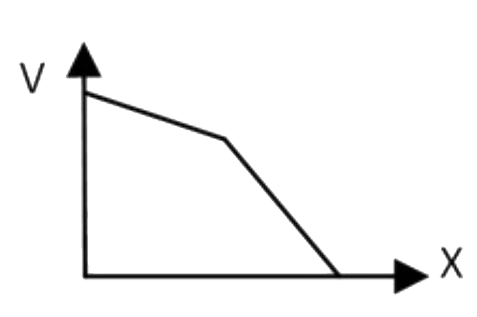
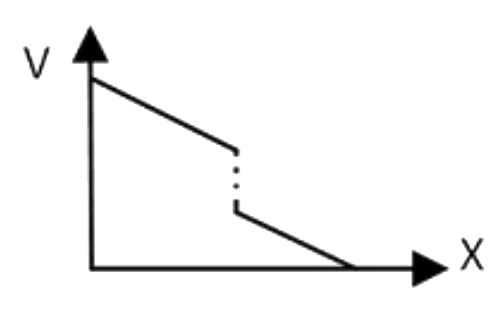
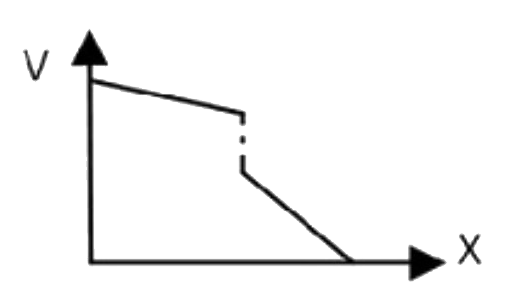
A
B
C
D
Text Solution
AI Generated Solution
The correct Answer is:
Similar Questions
Explore conceptually related problems
Recommended Questions
- Two cylindrical rods of same cross-section area and same length are c...
Text Solution
|
- A current I flows through a cylindrical rod of uniform cross-section a...
Text Solution
|
- Two rods of different materials having differnet lengths and same cros...
Text Solution
|
- Two rods of the same length and areas of cross-section A1 and A2 have ...
Text Solution
|
- Two rods are connected as shown. The rods are of same length and same ...
Text Solution
|
- A cylindrical solid of length L and radius a is connected across a sou...
Text Solution
|
- एक छड़ के पदार्थ का घनत्व rho=A+Bx के अनुसार बदलता है , जहाँ A,B अचर है...
Text Solution
|
- Two cylindrical rods of same cross-section area and same length are c...
Text Solution
|
- Two metallic rods are connected in series. Both are of same material o...
Text Solution
|